Я же правильно понимаю, что если кубоид совершенный, то каждая его грань даёт пифагорову тройку? То же самое с сечением каждой плоскостью, проходящей через параллельные рёбра, не?
-- 04.02.2018, 00:38 --Вообще, алгоритм перебора в лоб довольно прост. Берём очередную пифагорову тройку, задаваемую парой
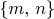
. Она образует основание кубоида (в плоскости Oxy). Берём диагональ полученного основания и раскладываем на множители, а потом смотрим на уравнение:

Находим, какие из этих двух уравнений решаются в целых числах, и какие получаются решения. Эти решения дают пифагоровы тройки, в которых один катет является диагональю основания, другой — высотой кубоида, а третий — пространственной диагональю. Все эти числа по построению целые. Осталось просто проверить диагонали двух других сторон. Затем следующее основание. Тут только их надо упорядочить в каком-нибудь разумном порядке.



