Наверное, нужно ещё раз напомнить про критерий успешности для Утки.
Если, например, у Утки критерий — минимизация времени доплытия до берега при условии, что Лиса её не ловит, то все рассуждения в этой теме нужно выкинуть и решать задачу заново.
Так что давайте лишний раз чётко заявим, что у Утки тот же критерий, что и у Лисы — расстояние между животными в момент достижения Уткой берега (Лиса пытается его минимизировать, а Утка — максимизировать).
Так вот, оптимальной траекторией для Утки после достижения "окружности безопасности" будет прямая, являющаяся касательной к этой окружности
только если Лиса ведёт себя оптимально, т.е. несётся с максимальной скоростью в одном и том же направлении (в каждый момент времени сокращающем расстояние до Утки).
Если Лиса отклоняется от своего оптимального поведения, то у Утки появляется возможность увеличить критерий. И тогда её оптимальная траектория (
уточню: вычисленная исходя из предположения, что в последующие моменты времени Лиса вернётся к своей оптимальной стратегии; т.е. Утка максимизирует гарантированный выигрыш) будет отлична от прямой.
Правда, когда Вы пишете:
wrest писал(а):
... если

?
то как-то совсем уж сильно ломаете исходную задачу, и уточнение в скобках в моём предыдущем предложении о том, что Лиса тут же вернётся к меньшей скорости

становится каким-то неестественным. Но если всё-таки его придерживаться (а если не его, то нужно что-то другое предположить явно, например, что Утке
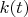
известно заранее), то получается, что Утка просто перевычисляет мгновенную цель на берегу и мгновенный вектор скорости направляет к этой точке (если Лиса возвращается к оптимальной стратегии, то мгновенный вектор сохраняется, и Утка снова плывёт по прямой). Особняком стоит случай, когда Утка и Лиса оказываются на одном диаметре (разумеется, с противоположных от центра сторон): в этот момент Утка не знает, в какую сторону Лиса побежит в следующий момент (локально любое направление оптимально), поэтому в этот (и только в этот) момент Утке выгоднее плыть по этому же диаметру к берегу (это будет её стратегией в течение ненулевого времени, если Лиса остановится на диаметре), тут же меняя свою стратегию, как только Лиса сходит с диаметра.



 от центра (радиус озера 1, скорость утки 1. скорость лисы - k), противоположную от лисы.
от центра (радиус озера 1, скорость утки 1. скорость лисы - k), противоположную от лисы. к ближайшей точке окружности, здесь r - величина удаления от центра.
к ближайшей точке окружности, здесь r - величина удаления от центра. , где
, где  находится из трансцендентного уравнения:
находится из трансцендентного уравнения:
 градусов и
градусов и 

 даёт то же самое число, но вот вид кривой вызывает сомнения. Я её численно промоделировал для
даёт то же самое число, но вот вид кривой вызывает сомнения. Я её численно промоделировал для  , получилось что утка совершает поворот на
, получилось что утка совершает поворот на  , проходя при этом дистанцию
, проходя при этом дистанцию  единиц. Но лиса при этом проходит
единиц. Но лиса при этом проходит  окружности, что для неё составляет лишь
окружности, что для неё составляет лишь  единиц длины, что очевидно меньше чем
единиц длины, что очевидно меньше чем  . Т.е. лиса успевает в точку встречи намного раньше утки. Беда однако.
. Т.е. лиса успевает в точку встречи намного раньше утки. Беда однако. на
на  в формуле угла (как поправлено в сообщении) даёт движение утки по прямой указанной Вами в самом первом сообщении (с постоянным
в формуле угла (как поправлено в сообщении) даёт движение утки по прямой указанной Вами в самом первом сообщении (с постоянным  ). Т.е. выходит что эта страшная формула траектории даёт
). Т.е. выходит что эта страшная формула траектории даёт  и направление скорости имеет угол
и направление скорости имеет угол  с радиус вектором.
с радиус вектором. она удаляется от центра на расстояние
она удаляется от центра на расстояние  и угол отклонения от лисы увеличивается на
и угол отклонения от лисы увеличивается на . Здесь вычли уменьшение угла за счет скорости Лисы.
. Здесь вычли уменьшение угла за счет скорости Лисы. максимально. Отсюда получается указанное соотношение.
максимально. Отсюда получается указанное соотношение. не как константу, а как функцию от времени
не как константу, а как функцию от времени  , по сути текущую скорость Лисы. Тогда вопрос. Если Лиса знает что у Утки вот такая стратегия, может Лиса догнать Утку или хотя бы сделать так что Утка не доплывет до берега?
, по сути текущую скорость Лисы. Тогда вопрос. Если Лиса знает что у Утки вот такая стратегия, может Лиса догнать Утку или хотя бы сделать так что Утка не доплывет до берега? , то
, то 
 ? По идее, тогда Утка должна двигаться удаляясь от берега?
? По идее, тогда Утка должна двигаться удаляясь от берега? ?
? становится каким-то неестественным. Но если всё-таки его придерживаться (а если не его, то нужно что-то другое предположить явно, например, что Утке
становится каким-то неестественным. Но если всё-таки его придерживаться (а если не его, то нужно что-то другое предположить явно, например, что Утке 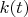 известно заранее), то получается, что Утка просто перевычисляет мгновенную цель на берегу и мгновенный вектор скорости направляет к этой точке (если Лиса возвращается к оптимальной стратегии, то мгновенный вектор сохраняется, и Утка снова плывёт по прямой). Особняком стоит случай, когда Утка и Лиса оказываются на одном диаметре (разумеется, с противоположных от центра сторон): в этот момент Утка не знает, в какую сторону Лиса побежит в следующий момент (локально любое направление оптимально), поэтому в этот (и только в этот) момент Утке выгоднее плыть по этому же диаметру к берегу (это будет её стратегией в течение ненулевого времени, если Лиса остановится на диаметре), тут же меняя свою стратегию, как только Лиса сходит с диаметра.
известно заранее), то получается, что Утка просто перевычисляет мгновенную цель на берегу и мгновенный вектор скорости направляет к этой точке (если Лиса возвращается к оптимальной стратегии, то мгновенный вектор сохраняется, и Утка снова плывёт по прямой). Особняком стоит случай, когда Утка и Лиса оказываются на одном диаметре (разумеется, с противоположных от центра сторон): в этот момент Утка не знает, в какую сторону Лиса побежит в следующий момент (локально любое направление оптимально), поэтому в этот (и только в этот) момент Утке выгоднее плыть по этому же диаметру к берегу (это будет её стратегией в течение ненулевого времени, если Лиса остановится на диаметре), тут же меняя свою стратегию, как только Лиса сходит с диаметра. , и даже знаем куда Утке надо плыть: по касательной к "кругу безопасности".
, и даже знаем куда Утке надо плыть: по касательной к "кругу безопасности". является функцией координат Лисы и Утки.
является функцией координат Лисы и Утки. утка может спокойно плыть прямо из центра по малой полуоси эллипса - лисе никуда сдвигаться невыгодно, любой её сдвиг увеличивает расстояние до утки, так она и останется в неподвижности. От соотношения скоростей не зависит.
утка может спокойно плыть прямо из центра по малой полуоси эллипса - лисе никуда сдвигаться невыгодно, любой её сдвиг увеличивает расстояние до утки, так она и останется в неподвижности. От соотношения скоростей не зависит.