Приближение натурального ряда разностями кортежа

[atlakatl]

Пусть $A=[k_1, k_2, ..., k_{a-1}, k_{a}]$ кортеж неотрицательных действительных чисел a-го порядка. Они образуют $p=a \cdot (a-1)/2$ шт. разностей $\left\lvert k_i-k_j\right\rvert$.
Попробуем максимально приблизить отрезок натурального ряда $(1, 2, ..., p-1, p)$ этими разностями. В качестве критерия оптимальности выберем $S=\sum\limits_{1}^{p}(\left\lvert k_i-k_j\right\rvert-n_r)^2$. Так при $a=3$ $k_1=0, k_2=1, k_3=3$, при $a=4$ $k_1=0, k_2=1, k_3=4, k_4=6$, абсолютно точно приближающие разностями свои отрезки.
Дальше полных совпадений не получается. Просто минимизируем $S$.
Численно задача решается трудно: локальные max и min образуют яичную ячейку, к тому же используются модули. Потому о гладкости функции можно забыть.
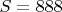
Остаётся случайный поиск. При $a=30$ и 50 млн. итераций достигается $S=888$. Это очень хорошая оценка. Интуитивно подбирая числа кортежа, вы будете получать $S=12000...25000$.

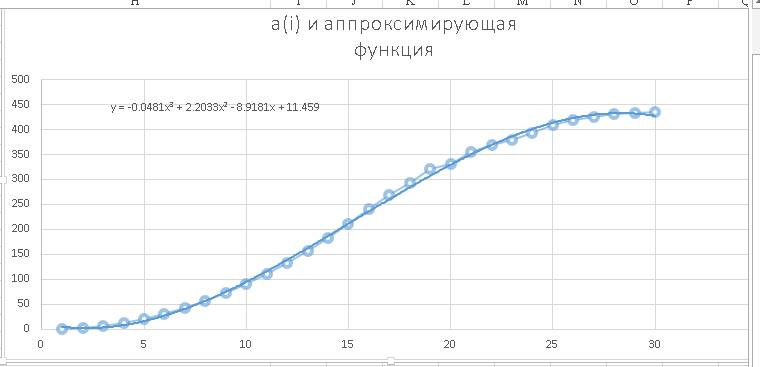
Правая и левая части функции явно симметричны. Однако при этой симметрии надо добиться максимальной ассимметрии разностей.
Случайный поиск себя исчерпал. Нужна какая-то концепция построения кортежа.
Есть ли методы для подобных задач?