Если переписать характеристическое уравнение в виде:

то для действительных

из графика понятно, что при нечетном

уравнение (1) имеет один действительный (положительный) корень, при

четном два действительных корня, положительный и отрицательный (положительный больше по модулю). Обозначим положительный корень уравнения (1) через

.
Для комплексных корней

из уравнения (1) следует неравенство:

Откуда следует, что
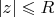
, причем равенство возможно, только если

действительное.
Таким образом асимптотика определяется положительным корнем

уравнения (1).