oleg_parhimchic, Ваша главная ошибка в том, что Вы ищете в математике какие-то правила, которым нужно строго следовать (типа "всегда перемножать крест накрест"); а надо пользоваться не правилами, а логикой.
Откуда, к примеру, возникает "правило" с "перемножением крест-накрест"? Например, так.
Надо сложить

.
Мы знаем, что если знаменатели дробей равны, то нужно сложить числители, а знаменатель оставить прежним: например,

. (К этому тоже надо относиться не как к какому-то "правилу", а надо понимать, почему это так; но сейчас не об этом.)
Что же делать, если знаменатели различны,
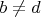
? Надо как-то преобразовать обе дроби, чтобы знаменатели у них стали равными.
И у нас есть инструмент для этого: мы знаем, что если умножить числитель и знаменатель на одно и то же число, то дробь не изменится. Если мы умножим числитель и знаменатель первой дроби на

, а второй на

, то у дробей как раз и окажется один и тот же знаменатель

, что нам и нужно. Поэтому:
 Вот это
Вот это надо понимать, а не учить какие-то "правила". И не только здесь, а по возможности повсюду, где только можно и где это получится.
Пусть теперь у нас такое задание: сложить

.
Вместо того, чтобы тупо "перемножать крест-накрест", можно попытаться порассуждать тем же способом, что и выше.
И увидеть, что если умножить числитель и знаменатель левой дроби на

, а правой на

, то знаменатель опять же получится один и тот же:

.
Таким образом,

(Наверняка, Вам рассказывали в классе пятом или шестом, как эти множители

и

найти не путём подбора, а с помощью чёткого алгоритма.
Стоит вспомнить. Что-то подобное Вам стоит делать и в Вашем задании).
Наконец. Если ответ получился не такой, как "в ответе" - это ещё не значит, что он неверный. Например, перемножив "крест-накрест", Вы получили
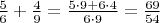
, а в ответе стоит почему-то

. Понимаете, почему это один и тот же ответ?