Здравствуйте! При анализе алгоритма с рекурсией получилось следующее рекуррентное соотношение

где

Для начала рассматриваю его в предположении что

кратно

. Предварительно вывел из комбинаторных соображений формулу для вычисления количества выполнений рекурсивной процедуры при длине данных

.

Потом решил пойти более строгим путем и вывести замкнутое выражение для решения данной рекуррентности через производящие функции. Выполнил стандартную процедуру из четырех этапов и на четвертом этапе получил следующее соотношение для производящей функции:

Согласно методу производящих функций для решения рекуррентных соотношений данную замкнутую форму производящей функции необходимо разложить в степенной ряд. Но знаменатель не раскладывается в общем случае на простые множители. Если же представлять данную функцию рядом Тэйлора то при длине данных например 100 или 200 придется брать производную от производящей функции соответствующего порядка что малореально.Подскажите пожалуйста, есть ли какой то иной способ представить данное соотношение
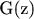
в виде степенного ряда или нужно было использовать какой - либо другой вид производящей функции с самого начала ?