Доброго дня,
заинтересовался теорией вероятностей, и начал с учебника Вентцель Е.С 1969 г.
На стр.65 приводится задача Пример 5:
Прибор состоит из 8 однородных элементов, но может работать при наличии
в исправном состоянии не менее 6 из них. Каждый элемент за время работы прибора

выходит из строя независимо от других с вероятностью

. Найти вероятность того, что прибор откажет за время

.
Решение: для отказа прибора требуется выход из строя
не менее двух из восьми элементов. По формуле

имеем:

Ответ по Вентцель Е.С.

.
------------
Мое решение:
По условию задачи имеем

элементов.
Сохраняющий работоспособность (

), если работают
не менее 6 элементов.
Т.е.

.
Не менее 6, значит 6, 7 или 8 элементов должны работать.
Предположим, что это

элементы работающие. 7 и 8 не работающие.
Чтобы прибор отказал по условию задачи необходимо чтобы работающих элементов стало
менее 6.
Т.е., для нашего случая, это выход любого элемента с номером

, т.е.

. Остается 5 элементов.
Прибор ломается, если осталось 5 элементов и меньше.
Чтобы работоспособных элементов оставалось
не менее 6, число отказавших элементов должно быть
не менее 3х, а не
не менее 2х, как в условиях задачи. Так как формулировка «не менее» 2х, включает 2.
Но устройство сохраняет работоспособность при 6 элементах, а два отказа приводят к тому, что еще 6 элементов рабочие.
Если ли тут в моих рассуждениях ошибка?
Выполнил расчет:
Таблица с расчетом в Excel доступна по ссылке:
https://yadi.sk/i/_FyX2vpy3RL9oKТаблица в png на яндекс.диске:
https://yadi.sk/i/2fnEWdnH3RLAiNРасчет показывает, что
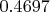
это вероятность сохранения работоспособности 6 элементов, или отказа 2х элементов.
В расчетах принято

, т.е. я считаю вероятность сохранения работоспособности элементов.
Мое решение:
Вероятность сохранения работоспособности не менее

, т.е. 6,7 или 8 элементов равна:

.
Вероятность отказа не менее 3х элементов равна

В чем моя ошибка в итоге?
Есть еще один пример в котором я сомневаюсь в Задачнике уже Вентцель. Чуть позже сформулирую и его.