Выпуклая оболочка суммы Минковского

[ikozyrev]

Решаю задачку для первого курса:
Доказать что выпуклая оболочка суммы Минковского двух множеств $conv(S_1+S_2)$ равна сумме Минковского выпуклых оболочек этих множеств $conv(S_1)+conv(S_2)$, $S_1, S_2\in A(V).$
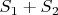
Включение в одну сторону очевидно: по теореме Каратеодори, любую точку выпуклой оболочки множества $S_1+S_2$ мы можем представить как выпуклую комбинацию конечного (нам в данном случае интересна конечность) набора точек этого множества, каждая из которых представляется в виде суммы точек из $S_1$ и $S_2$:
$p\in conv(S_1+S_2) = \lambda_1(x_1+y_1)+{\lambda_2}(x_2+y_2)+...+{\lambda_k}(x_k+y_k) =$
$ ({\lambda_1}x_1+{\lambda_2}x_2+...+{\lambda_2}x_k) + ({\lambda_1}y_1+{\lambda_2}y_2+...+ {\lambda_2}y_k)= x+y$
где $x, y$ - точки принадлежащие выпуклой оболочке $S_1$ и $S_2$ соответсвенно и $\sum\limits_{i}^{}\lambda_i=1$, $\lambda_i\geqslant 0$.
Некоторые $x_i$ могут совпадать с некоторыми $x_j$ а некоторые $y_i$ с некоторыми $y_j$ но сути это не меняет.

А вот в обратную сторону не могу понять как делать: Пробую опять воспользоваться Теоремой Каратеодори, тогда получаем две точки из выпуклых оболочек $S_1$ и $S_2$:
$x={\alpha_1}x_1+{\alpha_2}x_2+...+{\alpha_k}x_k$, $\sum\limits_{i}^{}\alpha_i=1$, $\alpha_i\geqslant0$
$y={\beta_1}y_1+{\beta_2}y_2+...+{\beta_k}y_k$ , $\sum\limits_{i}^{}\beta_i=1$, $\beta_i\geqslant0$
и их сумма:
$z={\alpha_1}x_1+{\beta_1}y_1+...+{\alpha_k}x_k+{\beta_k}y_k$

Но как доказать теперь что $z$ принадлежит $conv(S_1+S_2)$?
Идея в том чтобы привести $z$ к выражению:
$z={\gamma_1}(x_1+y_1)+{\gamma_2}(x_2+y_2)+...+{\gamma_k}(x_k+y_k)$, $\sum\limits_{i}^{}\gamma_i=1$,$\gamma_i\geqslant0$
но как это сделать я не понимаю...

[svv]

ikozyrev в сообщении #1281958 писал(а):

Идея в том чтобы привести $z$ к выражению:
$z={\gamma_1}(x_1+y_1)+{\gamma_2}(x_2+y_2)+...+{\gamma_k}(x_k+y_k)$, $\sum\limits_{i}^{}\gamma_i=1$,$\gamma_i\geqslant0$

Нет, необязательно к такому. Пусть $A=\bigcup\limits_{i=1}^m \{x_i\}, B=\bigcup\limits_{j=1}^n \{y_j\}$, тогда $A+B$ будет состоять из точек
$z_{ij}=x_i+y_j,\quad 1\leqslant i \leqslant m,\quad 1\leqslant j \leqslant n$,
а не только из точек $z_{ii}=x_i+y_i$.
А из такого широкого набора точек Вы, несомненно, слепите выпуклую комбинацию $z=\sum\limits_{i,j}\gamma_{ij}z_{ij}$, равную $x+y$.

[ikozyrev]

svv в сообщении #1282020 писал(а):

Нет, необязательно к такому. Пусть $A=\bigcup\limits_{i=1}^m \{x_i\}, B=\bigcup\limits_{j=1}^n \{y_j\}$, тогда $A+B$ будет состоять из точек
$z_{ij}=x_i+y_j,\quad 1\leqslant i \leqslant m,\quad 1\leqslant j \leqslant n$,
а не только из точек $z_{ii}=x_i+y_i$.
А из такого широкого набора точек Вы, несомненно, слепите выпуклую комбинацию $z=\sum\limits_{i,j}\gamma_{ij}z_{ij}$, равную $x+y$.

Да, я тоже думал в этом направлении уже. Вот теперь мучаюсь как же это слепить.

[svv]

$\gamma_{ij}=\alpha_i \beta_j$
Докажите, что при этом $z=x+y$ и $\sum\limits_{i,j}\gamma_{ij}=1$.

[ikozyrev]

svv в сообщении #1282075 писал(а):

$\gamma_{ij}=\alpha_i \beta_j$
Докажите, что при этом $z=x+y$ и $\sum\limits_{i,j}\gamma_{ij}=1$.

Круто. Действительно там все под знаком суммы выходит прям как надо.
У меня только один вопрос - как вот так сходу можно догадаться? :)
Я бы хотел дойти до такого уровня чтобы видеть сразу такие решения.