Парадокс Гиббса

[ShSV]

Здравствуйте!
Предлагаю обсудить зависимость энтропии не от объёма, занимаемого одной частицей, а от длины свободного пробега. Ведь именно длина свободного пробега определяет термодинамические свойства.


Вот моё решение классического парадокса Гиббса.
Описание в Википедии:
https://ru.wikipedia.org/wiki/%D0%9F%D0 ... 1%81%D0%B0

«Обычно выход из тупика там же, где и вход» - народная мудрость :)

Энтропия идеального газа выражается формулой:
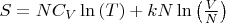
$S = N {C_V} \ln{\left({T}\right)} + k N \ln{\left(\frac {V}{N}\right)}$ (1),
где
$S$ – энтропия,
$N$ — количество частиц,
$C_V$ - теплоёмкость при постоянном объёме,
$T$ – температура,
$k$ — постоянная Больцмана,
$V$ – объём.

Рассматривают два одинаковых объёма газов с одинаковыми $T$ и $N$, между которыми перегородка. Перегородку убирают. В первом случае смешивают два одинаковых газа; во втором - два почти не отличающихся различных газа. Получаются энтропии с разницей в $2 k N \ln{\left(2\right)}$ (2) .
В экспериментах никакой разницы нет!
Выход из этого тупика будем искать там же, где и вход. А именно, в формуле (1).
Заметим, что длина свободного пробега частиц равна:
$L = \frac {1}{\sqrt{2} \sigma \frac {N}{V}}$ (3),
где
$L$ — длина свободного пробега частиц,
$\sigma$ — площадь поперечного сечения одной частицы.

Тогда формула (1) преобразуется к виду:
$S = N {C_V} \ln{\left({T}\right)} + k N \ln{\left(\sqrt{2} \sigma L \right)}$ (4).

При смешении что одинаковых газов, что почти похожих, длина свободного пробега частиц ($L$) не меняется. Поэтому и энтропии этих газов ведут себя одинаково.
Что решает классический парадокс Гиббса.

Всем наилучших пожеланий!
Счастья и здоровья!

[photon]

Тема перемещена из форума «Физика» в форум «Карантин»
по следующим причинам:

- неправильно набраны формулы (краткие инструкции: «Краткий FAQ по тегу [math]» и видеоролик Как записывать формулы) - исправьте запись отдельных переменных, а также знака логарифма;
- непонятно, что именно вы хотите обсудить. Если свой вариант разрешения парадокса, то ему, думаю, место в дискуссионном разделе.

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.