Сферическая планиметрия (сферометрия?)

[arseniiv]

(Не про сферическое)

B@R5uk в сообщении #1280273 писал(а):

Ну, мне для понимания что значит "снаружи" такая точка нужна.

А, ну для как раз аффинной (в которой нет точек, о которых можно было бы сказать, что они бесконечно удалены), а не проективной плоскости всё просто, выпуклая оболочка множества $S$ — это наименьшее по включению выпуклое множество, содержащее $S$, и если $S$ ограничено, в. о. будет тоже ограниченной. А ограниченность тоже определяется без всяких бесконечно удалённых точек — это значит, что множество целиком влезает в некоторый шар (в случае плоскости — круг).

Интуиция у этого определения (применимого для любого метрического пространства) такая, что всякий круг имеет конечный радиус, и ему вполне позволительно потому называться ограниченным, ну а если что-то уместилось в чём-то ограниченном, оно тоже должно быть ограниченным.

[B@R5uk]

grizzly в сообщении #1280279 писал(а):

Пусть задана окружность и точка на её южном полюсе.

Это самый плохой случай, который только можно придумать. Выродились и объединились в одно целых два разных решения, одно — в отрезок (а должно быть эллипсом), а другое — в луч (а была ветвью гиперболы).

Итак, задача. На плоскости заданы окружность и точка. Необходимо определить, что из себя представляет ГМТ, равноудалённых от заданных окружности и точки.

Решение. Разместим начало декартовых координат в центре окружности, ось Ox направим через заданную точку. Обозначим радиус окружности $R$, а x-координату исходной точки — $a$. Тогда уравнение ГМТ примет вид:

$$\left| \sqrt{{{x}^{2}}+{{y}^{2}}}-R \right|=\sqrt{{{\left( x-a \right)}^{2}}+{{y}^{2}}}$$

Решая его находим:

$$\[\frac{{{\left( x-{a}/{2}\; \right)}^{2}}}{{{\left( {R}/{2}\; \right)}^{2}}}+\frac{{{y}^{2}}}{{{\left( {R}/{2}\; \right)}^{2}}-{{\left( {a}/{2}\; \right)}^{2}}}=1\]$$

С дополнительным ограничением:

$$\[x>\frac{{{a}^{2}}-{{R}^{2}}}{2a}\]$$

То есть искомое ГМТ — это либо эллипс, либо ветвь гиперболы, в зависимости от того, как расположены исходная окружность и точка. Если точка внутри — то эллипс, иначе — гипербола. В случае, когда точка лежит на окружности, решением является положительная координатная полусь Ox.

Вопрос о том, что будет на сфере, пока открыт. Хотелось бы, чтобы было что-нибудь простое.

[Pphantom]

Как-то у вас тут все очень сложно...

Пусть на сфере есть окружность и точка. Не умаляя общности, можно считать, что окружность - параллель в какой-то сферической системе координат (и, соответственно, она полностью определяется широтой $\varphi_1$ в этой СК). Где бы не лежала точка, у нее в той же СК есть некоторая широта $\varphi_2$ и некоторая долгота, которую можно выбирать произвольным образом (и давайте для удобства выберем ее равной нулю). Теперь для произвольной точки с координатами $(\varphi,\lambda)$ условие равноудаленности от окружности и точки означает, что $|\varphi-\varphi_1| = \arccos (\sin \varphi \sin \varph_2 + \cos \varphi \cos \varphi_2 \cos \lambda)$. Отсюда

$$\tg \varphi = \frac{\cos\varphi_1 - \cos\varphi_2 \cos \lambda}{\sin\varphi_2 - \sin\varphi_1}$$

и это в общем-то явное уравнение искомой кривой.

[grizzly]

(Оффтоп)

B@R5uk в сообщении #1280294 писал(а):

Это самый плохой случай, который только можно придумать. Выродились и объединились в одно целых два разных решения, одно — в отрезок (а должно быть эллипсом), а другое — в луч (а была ветвью гиперболы).

Да, всё так. С эллипсом внутри я там ошибся, конечно -- он тоже вырождается.

[slavav]

Описания прямого алгоритма на сфере у меня нет. Но он отличается от плоского алгоритма лишь в деталях и примитивах (примитивом я называю элементарную операцию: принадлежность точки полуплоскости или определение пересечения отрезков).
Предлагаю такую схему: разберите плоский алгоритм по вашему выбору, затем мы обсудим его перенос на сферу.

[B@R5uk]

Pphantom в сообщении #1280300 писал(а):

и это в общем-то явное уравнение искомой кривой.

Действительно всё просто. Только я люблю сферическую систему координат, где угол тета отсчитывается от оси Oz. Потому у меня так:

$$\left| \theta -{{\theta }_{1}} \right|=\arccos\left( \cos \theta \cos {{\theta }_{2}}+\sin \theta \sin {{\theta }_{2}}\cos \varphi \right)$$

$$\cot \theta =\frac{\sin {{\theta }_{1}}-\sin {{\theta }_{2}}\cos \varphi }{\cos {{\theta }_{2}}-\cos{{\theta }_{1}}}$$

Я так же предпочитаю арктангенс двух переменных любой другой обратной тригонометрической функции:

$$\[\theta ={\arctg}_{2}\left( \sin {{\theta }_{2}}\cos \varphi -\sin {{\theta }_{1}},\cos {{\theta }_{2}}-\cos{{\theta }_{1}} \right)+\frac{\pi }{2}\operatorname{sgn} \left( {{\theta }_{1}}-{{\theta }_{2}} \right)\]$$

Осталось только понять, являются ли эти фигуры сферическим аналогом плоского эллипса? И вообще, существует ли на сфере аналоги плоских конических сечений?

[arseniiv]

B@R5uk в сообщении #1280343 писал(а):

Осталось только понять, являются ли эти фигуры сферическим аналогом плоского эллипса? И вообще, существует ли на сфере аналоги плоских конических сечений?

Смотря в чём аналоги. Например, все кривые второго порядка из евклидова пространства, полностью находящиеся на погружённой туда сфере — это окружности. А можно рассматривать пересечения конуса со сферой аналогично пересечению конуса с плоскостью. И наверняка ещё что-нибудь.

[B@R5uk]

arseniiv в сообщении #1280369 писал(а):

Смотря в чём аналоги.

Да, это тоже важный вопрос. Например, для эллипса первое свойство, которое я в своё время узнал, связанно с постоянством суммы расстояния от фокусов эллипса до любой его точки (откуда следует возможность его построения с помощью двух кнопок, петли из нитки и карандаша). И судя по всему, для построенного ГМТ это свойство выполняется. Фокусами сферического эллипса являются серверный или южный полюс и заданная в условии точка (не зря мне так и хотелось назвать её фокусом). Суммой расстояний до фокусов является расстояние от северного или южного полюса до заданной окружности. Доказательство этого факта следует из полной идентичности уравнений для одного и для другого рассмотрения. Просто для ГМТ там есть модуль, а для эллипса его нет. Раскрытие модуля зависит от взаимного расположения окружности и точки, поэтому вторым фокусом будет либо северный, либо южный полюс.

То есть ГМТ является самым настоящим сферическим эллипсом!

-- 31.12.2017, 17:09 --

Если взять в качестве фокусов сферического эллипса точки $\left(\theta_1, 0\right)$ и $\left(\theta_1, \pi\right)$ и записать его уравнение:

$$\arccos\left( \cos \theta \cos {{\theta }_{1}}+\sin \theta \sin {{\theta }_{1}}\cos \varphi \right)+\arccos\left( \cos \theta \cos {{\theta }_{1}}-\sin \theta \sin {{\theta }_{1}}\cos \varphi \right)=\alpha $$

А затем его попреобразовывать и воспользоваться связью с декартовыми координатами, по получится такое выражение:

$$\[2{{z}^{2}}\left( 1-\cos\alpha \right){{\cos }^{2}}{{\theta }_{1}}+2{{x}^{2}}\left( 1+\cos\alpha \right){{\sin }^{2}}{{\theta }_{1}}={{\sin }^{2}}\alpha \]$$

То есть сферический эллипс является одной из половинок сечения сферы эллиптическим цилиндром, ось которого проходит через центр сферы.

Хотя такое рассмотрение мне концептуально не очень нравится. Сфера — это само по себе пространство, с трёхмерным ничего общего не имеющее, нам просто удобно изучать сферическую геометрию, погружая сферу в евклидово трёхмерие. Если уж строить полную аналогию, то сферическое пространство надо сначала как-то обобщить, добавив ему ещё одно измерение, затем в полученном криволинейном пространстве строить аналоги конуса и секущей плоскости и смотреть получается ли там желаемое или нет.

[B@R5uk]

А как сгенерировать случайный угол тета так, чтобы результирующее распределение точек на сфере было равновероятным. Угол фи при этом должен быть равномерно распределён на отрезке $\left[-\pi,\pi\right]$. У меня есть генератор случайных чисел с равномерным распределением на отрезке $\left[0,1\right]$, какую я должен взять от него функцию, чтобы получить желаемое распределение для тета? Я правильно понимаю, что мне надо желать такую функцию распределения для тета, чтобы она была пропорциональна длине окружности с соответствующим углом, то есть величине $\sin\theta$?

-- 01.01.2018, 11:30 --

Нашёл решение: topic8992.html Если обозначить результат генератора случайных чисел как икс, то формула будет такой (угол тета отсчитывается от направления оси Oz):

$$\theta=\arccos\left(2x-1\right)$$

[INGELRII]

B@R5uk в сообщении #1280294 писал(а):

Необходимо определить, что из себя представляет ГМТ, равноудалённых от заданных окружности и точки.

Расстояние от точки до окружности и расстояние от той же точки до центра этой окружности связаны друг с другом довольно очевидным соотношением. Если подумать об этом пару секунд, то ваш результат перестает быть таким уж удивительным.

[B@R5uk]

INGELRII в сообщении #1280499 писал(а):

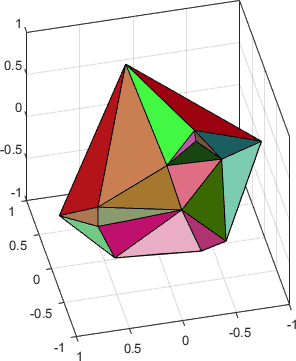
результат перестает быть таким уж удивительным

Да, согласен. Но результату, полученному на плоскости я и не удивлялся. За то результат на сфере в этом плане гораздо более интересен. Хотя логика всё равно остаётся той же самой.

slavav в сообщении #1280340 писал(а):

Предлагаю такую схему: разберите плоский алгоритм по вашему выбору, затем мы обсудим его перенос на сферу.

Проблема в том, что я не знаю даже за что взяться. В книге O'Rourke - Computational Geometry in C, которую вы предложили, подробно разбирается только алгоритм, в котором диаграмма Вороного строится через выпуклую оболочку точек, получаемых проецированием с плоскости на трёхмерный параболоид. Со сферой в этом плане даже ничего проецировать не надо: погружаем в трёхмерие и стоим выпуклую оболочку. Однако алгоритм для построения выпуклой оболочки в трёхмерии не использует тот факт, что среди всех точек сферы никогда не найдётся такой, что она окажется внутри оболочки. Этот факт вообще может как-то упростить вычисления?

Брутфорсом выпуклую оболочку построить легко. В матлабе это дело даже хорошо векторизуется и занимает четыре строчки:

Используется синтаксис Matlab M

function indexes = get_convex_hull_brute(thetas, phis)

dsize = numel(thetas);
indexes = [nchoosek(1 : dsize, 3) flipud(nchoosek(1 : dsize, dsize - 3))];
flags = is_internal(thetas(indexes), phis(indexes));
indexes = indexes(0 == sum(flags, 2), 1 : 3);

end

Здесь, правда, всё нагрузка ложится на функцию is_internal, которая для каждой строчки координат точек через первые три точки проводит окружность, а для остальных определяет, лежат ли они внутри этой окружности или нет. Для 50 точек расчёт уже занимает секунду, поэтому надо улучшать алгоритм.

Но пока не совсем понимаю, как из полученной триангуляции строить вершины диаграммы Вороного. Если центр описанной окружности лежит внутри треугольника, то всё понятно: он и есть вершина. А что, если не лежит? Такие случаи скорее даже правило, чем исключение:

[arseniiv]

B@R5uk в сообщении #1280485 писал(а):

А как сгенерировать случайный угол тета так, чтобы результирующее распределение точек на сфере было равновероятным.

Можно вместо сферических координат сгенерировать три нормально распределённые величины $X,Y,Z$ (перегенерировать, если все вышли нулевыми) и отнормировать вектор $(X,Y,Z)$, это и будет равномерно распределённая на сфере точка. Также работает и для любой другой размерности.

[Pphantom]

arseniiv в сообщении #1280533 писал(а):

Можно вместо сферических координат сгенерировать три нормально распределённые величины $X,Y,Z$ (перегенерировать, если все вышли нулевыми) и отнормировать вектор $(X,Y,Z)$, это и будет равномерно распределённая на сфере точка. Также работает и для любой другой размерности.

Как вариант: генерировать три величины с плоским распределением в интервале $[-1;1]$, если модуль вектора $(X,Y,Z)$ больше единицы, результат просто выкидывать, если меньше - нормировать на единицу. Технически это быстрее.

[arseniiv]

Да, хороший вариант для малого числа измерений (для большого-то отбрасывыть придётся слишком часто), хотя что касается быстроты, так есть некоторые очень быстрые способы нагенерировать кучу стандартно нормально распределённых величин. Заканчивая всякими там зиккуратами.

[Pphantom]

arseniiv в сообщении #1280548 писал(а):

Да, хороший вариант для малого числа измерений (для большого-то отбрасывыть придётся слишком часто),

Да, конечно, но для размерности 3 он вполне годится.

arseniiv в сообщении #1280548 писал(а):

хотя что касается быстроты, так есть некоторые очень быстрые способы нагенерировать кучу стандартно нормально распределённых величин. Заканчивая всякими там зиккуратами.

С зиккуратом получается примерно так же, а все остальное обычно работает медленнее (опять-таки для размерности 3).