1.Show that if

is a point which does not belong to the closed point set

then
there exist mutually exclusive open sets OP and OM containing point

and

respectively.
2.Show that if H and K are mutually exclusive closed point sets then there exist mutually exclusive
open sets OH and OK containing H and K, respectively
Дорогие друзья, надеюсь Вас не смутила формулировка задачи на английском. Оригинал приведен для полной точности моей передачи. Итак, в первой части необходимо построить открытые множества
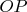
и
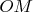
так, чтобы они включали в себя точку

и

, соответственно. В условии задано, что

- замкнутое множество, не содержащее

.
Мы можем построить открытые множества, если расстояние

будет больше нуля, тогда за радиус круга вокруг точки

возьмем

, а открытое множество
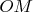
будет сформировано из объединений кругов с радиусом

вокруг каждой точки этого множества.
Теперь следует доказать, что

.
Докажем от противного. Пусть

, тогда для любого сколь угодно малого \varepsilon найдется такая точка из

, что
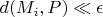
. А это уже определение предельной точки.
Как все мы знаем, замкнутое множество содержит свои предельные точки, значит расстояние точно не равно нулю.
К сожалению, это доказательство не работает для второй части утверждения, поскольку мы имеем два закрытых множества. Возьмем к примеру два множества, которые стремятся к асимптоте, приближаясь к ней на сколь угодно малое расстояние. Тогда мы не сможем найти такое

, следовательно,

.
Хочется взять в качестве открытых множеств множества, чуть более широкие, чем данные, и чуть быстрее устремляющиеся к асимптоте. Но здесь у меня возникает вопрос. Как их задать и как доказать их существование (возможность их построения)
Заранее благодарю.
P.S. Если текст вышел кривой, прошу отнестись с пониманием, пишу на dxdy впервые.
Ваш,
gleb_N