Добрый день, на этот раз решаю задачу:
Цитата:
Найти всевозможные пары чисел x и y таких, что среднее арифметическое чисел

,

,
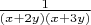
, ... ,

равно
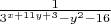
Для начала я нашел среднее арифметическое этих 10 чисел.
Т.к.

;
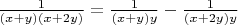
; ... ;

, то

Тогда

Теперь решаем целочисленное уравнение:


Решил проанализировать четность:
Выражение

имеет такую же четность как и

, т.к.
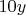
- чётное,

совпадает с четностью

. Если

- чётно, то и произведение

- чётно, аналогично, если

- нечётно, то и

- нечётно.
Выражение
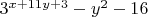
по чётности различается с

, т.к.

- нечётно. И если

- чётно, то всё выражение нечётно, иначе, если

- нечётно, то всё выражение чётно.
Тогда мы получаем, что числа

и

должны быть разной чётности. Тогда степень тройки

всегда чётная. Однако этим воспользоваться далее не получается ... Подскажите пожалуйста направление ... Спасибо



