Для двух базисов идеала аффинные многообразия совпадают

[Aoizora]

Пусть $f_1, \cdots, f_s$ и $g_1, \cdots, g_t$ - базисы одного и того же идеала в $k[x_1,\cdots,x_n]$, так что $\left\langle f_1,\cdots,f_s \right\rangle=\left\langle g_1,\cdots,g_t \right\rangle$. Доказать, что тогда $V(f_1,\cdots,f_s)=V(g_1,\cdots,g_t)$.

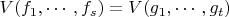
Я попытался использовать тот факт, что многочлены одного базиса выражаются через многочлены другого базиса. Пусть многочлены первого базиса выражаются через многочлены второго. Я расписал это в виде сумм. Как теперь доказать, что равны многообразия?

На данный момент известно только определение идеала, идеала, порожденного множеством, лемма о том, что множество, порожденное многочленами - это идеал, интерпретация идеала как выше как множество полиномиальных следствий системы уравнений, определенной базисными элементами, и все. Должно хватить этого, но у меня не получается.

[vpb]

Трудно сказать, в чем проблема, почему Вы этого не понимаете. Это нечто чрезвычайно простое. Напишите, какие книжки и какие места в этих книжках Вы по этому поводу читали.

[Aoizora]

vpb в сообщении #1278303 писал(а):

Трудно сказать, в чем проблема, почему Вы этого не понимаете. Это нечто чрезвычайно простое. Напишите, какие книжки и какие места в этих книжках Вы по этому поводу читали.

Это задание из книги Cox, Little, O'Shea "Многообразия, идеалы, алгоритмы". Читаю ее. До этого учился на алгебраической специальности для инженеров, но многое уже забылось.

[vpb]

Хорошо, это уже нечто более конкретное. Сейчас подумаю, что Вам посоветовать. (Или может кто-то другой посоветует, пока я думаю).

-- 24.12.2017, 17:16 --

Aoizora
В Литл-Кокс-О'Ши это утверждение на стр.48. Почему у Вас с ним трудности, понять так и не могу. В соответствии с тем, как принято на этом форуме, попробуем по шагам. Для начала, пусть имеем две переменные, $x_1$, $x_2$. Приведите пример, какой-нибудь, четырех многочленов $f_1,f_2,g_1,g_2\in k[x_1,x_2]$, (пусть скажем $k={\mathbb R}$), для которых $\langle f_1,f_2\rangle=\langle g_1,g_2\rangle$.

-- 24.12.2017, 17:17 --

[Aoizora]

Попробую. Пусть один из базисов $x,y$. Имеем идеал $\left\langle x,y \right\rangle$. Второй базис я получаю умножением базисных многочленов $x$ и $y$ на многочлены $x^2 - y$ и $y^2$. Получаю $\left\langle x^3 - xy,y^3 \right\rangle$. Линейная независимость, как я понимаю, не требуется. Наверное, неправильно.

[vpb]

Нет, неправильно. Вспомните определение базиса идеала и напишите сюда.

[Aoizora]

Базис идеала это такой набор элементов, что множество конечных линейных комбинаций этих элементов с полиномами кольца образует идеал.

[vpb]

Правильнее писать "множество конечных линейных комбинаций этих элементов, коэффициенты в которых --- произвольные элементы кольца". А еще лучше записывать то же, используя символы: "множество конечных линейных комбинаций вида $a_1f_1+\ldots+a_kf_k$, где $a_1,\ldots,a_k$ --- произвольные элементы кольца", примерно так.

Ну ладно. Как Вы думаете, $x$ является линейной комбинацией $x^3-xy$ и $y^3$ ? Если да, приведите эту комбинацию, если нет --- обоснуйте, почему.

[Aoizora]

Нет, не является. Коэффициент перед вторым многочленом должен быть нулевым многочленом. Подходящий коэффициент для первого многочлена подобрать нельзя.

[vpb]

Пожалуйста, напишите это более подробно и с некоторым числом символов, чтобы я убедился, что Вы правильно понимаете.

[Aoizora]

Запишем линейную комбинацию: $f(x,y)\cdot (x^3 - xy) + g(x,y) \cdot y^3 = x$. Нам нужно подобрать такие $f(x,y)$ и $g(x,y)$, чтобы равенство выполнялось. В правой части должен отсутствовать $y$, поэтому коэффициент $g(x,y)$ должен быть нулевым. Невозможно подобрать такой $f(x,y)$, чтобы $y^3$ взаимно уничтожился. Также мы не сможем подобрать такой $f(x,y)$, чтобы сумма равнялась $x$.

[vpb]

Aoizora в сообщении #1278375 писал(а):

В правой части должен отсутствовать $y$

Он в правой части и так отсутствует (правая часть --- это $x$). Вы хотели сказать, в правой части $y$ отсутствует, поэтому и в левой его быть не должно?

[Aoizora]

Да, именно это я и хотел сказать. И поскольку нельзя подобрать такой $f(x,y)$, чтобы $y^3$ сократился, мы берем $y^3$ с коэффициентом 0.

[vpb]

Aoizora в сообщении #1278387 писал(а):

нельзя подобрать такой $f(x,y)$, чтобы $y^3$ сократился

Не совсем понятно, что Вы под этим в виду имеете. Сократиться может одно слагаемое с другим, или, скажем, числитель со знаменателем, а тут что-то другое.

[Aoizora]

Имею в виду, что в произведении $f(x,y)\cdot (x^3 - xy)$ могли бы получиться такие члены, что $y^3$ сократился бы. Здесь это невозможно. Ладно, подскажете, как мне мыслить дальше?