Знакомая всем запись ВТФ

разбивает множество степеней на три случая:

, первый из которых малоинформативен, а третий требует доказательства. Второй же позволяет явно увидеть условия выполнения равенства

. Получим их.
Договоримся, что

.
Первое условие - равенство (

-мерных) объёмов, оно очевидно:

.
Второе условие - равенство путей. Чтобы получить его представим величины

и

трапециями (криволинейными в случае

) с основаниями

и

соответственно.
Пусть имеется начальный (дискретный) треугольник площадью

с основанием

.
Очевидно, что если пошагово двигать это основание в положительном направлении сохраняя его величину, то площадь опирающейся на него трапеции (в которую перейдёт треугольник уже на первом шаге) будет неограниченно увеличиваться. Но это запрещено равенством объёмов (в данном случае - площадей) – площадь начального треугольника должна равняться площади конечной трапеции. Таким образом, для соблюдения этого условия основание конечной трапеции должно быть меньше основания начального треугольника, что и выполняется в любой пифагоровой тройке: при

всегда

. Это значит, что при движении основание начального треугольника пошагово сокращается до тех пор, пока не сравняется с основанием конечной трапеции.
Однако, число шагов одинаково для обоих (левого и правого) краёв начального основания

. Это число – тактовое (дискретное) время
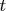
за которое площадь начального треугольника, сначала возрастая и потом убывая, возвращается к своему исходному значению. Из этого следует, что пути, которые проходят левый и правый края начального основания, имеют общий делитель и тактовое время равно их НОД:

. Это действительно выполняется в любой пифагоровой тройке. Соответственно, скорости левого и правого краёв начального основания имеют значения

.
При этом, на шаге  левый край начального основания догонит его правый край
левый край начального основания догонит его правый край.
Сделаем следующие замены:

- начальное основание (треугольника),

- конечное основание (трапеции),

- путь левого края начального основания (левый путь),

- путь правого края начального основания (правый путь),

- скорость левого края начального основания (левая скорость),

- скорость правого края начального основания (правая скорость),

- тактовое время (наибольший общий делитель левого и правого путей).
Теперь мы можем явно указать второе условие - равенство путей:

Далее, пользуясь полученными условиями, - условием равенства объёмов и условием равенства путей - можно получить общее условие существования пифагоровой тройки. Оно таково:

и должно выполняться в натуральных числах.
В случае первой степени скорости левого и правого краёв начального основания одинаковы и его величина сохраняется при любом времени движения.
Сравнение поведения скоростей в случаях

и

заставляет предположить, что в случае

к тактовым скоростям добавятся тактовые ускорения

и

. ВТФ утверждает, что при этом выполнение условия равенства объёмов невозможно. Как ускорения

и

повлияют на условие равенства путей я пока не вполне понимаю.
P.S. Условие равенства путей

можно интерпретировать иначе считая НОД

не временем, а скоростью. Тогда края начального основания будут проходить свои пути с одинаковой скоростью, но за разное время и условие примет вид

. Его смысл в этом контексте не ясен, но любопытна аналогия с локальными временами в специальной теории относительности.
P.P.S. Удалось привести некоторые степенные выражения к матричному виду. Пусть

- матрица показателя степени,
и

- матрица основания степени (для числа

- аналогично),

- ко- и контравариантные первые орты (вырезают из матрицы левый верхний элемент).
Тогда






