Система уравнений с тремя неизвестными

[Pripyat]

Добрый день, вот такая задача попалась:

$$\left\{ \begin{array}{rcl} x^4+x^3+x^2=z-1 \\ y^4+y^3+y^2=x-1 \\ z^4+z^3+z^2=y-1 \\ \end{array} \right.$$

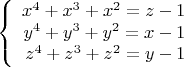
Стал решать так: преобразовал к виду:

$$\left\{ \begin{array}{rcl} x^4+x^3+x^2 + 1=z \\ y^4+y^3+y^2 + 1=x \\ z^4+z^3+z^2 + 1=y \\ \end{array} \right.$$

$$\left\{ \begin{array}{rcl} z = f(x)\\ x = f(y) \\ y = f(z)\\ \end{array} \right.$$

Здесь $f(t) = t^4+t^3+t^2 + 1 $.
Потом долго думал и решил сравнить аргумент и функцию, т.е. $x\wedge f(x)$
$ x^4+x^3+x^2 + 1 \wedge x$
$ x^4+x^3+x^2 - x+ 1 \wedge 0$
$ x^2 (x^2+x+\frac{1}{4}) + \frac{x^2}{2}+ (\frac{x^2}{4} - x+ 1) \wedge 0$
$ x^2 (x+\frac{1}{2})^2 + \frac{x^2}{2}+ (\frac{x}{2} - 1)^2 \wedge 0$
Получили сумму трёх квадратов, которая неотрицательная. Причём равна нулю только тогда, когда все три одновременно равны 0.
Здесь видно, что все три они одновременно не равны нулю. Получаем, что $ x^2 (x+\frac{1}{2})^2 + \frac{x^2}{2}+ (\frac{x}{2} - 1)^2 > 0$.
Тогда $ x^4+x^3+x^2 + 1 > x$, т.е. $ f(x) > x$.

$$\left\{ \begin{array}{rcl} z = f(x) >x\\ x = f(y) > y \\ y = f(z) > z\\ \end{array} \right.$$

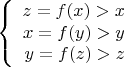
И здесь я получаю противоречие: z > x > y > z, чего быть не может и система получается решений не имеет. В принципе, ответ такой конечно может быть, но ощущение, что где-то ошибка.
Прошу развеять сомнения или направить на путь истинный. Спаисбо

[ИСН]

Всё так.

[gris]

Мне вторая система понравилась. В ней все правые части больше единицы, а значит и левые. Предположим, что существует решение. И какое-то значение на меньше остальных двух. Возможно-ль? Ну то есть тоже самое, только через минимум.
Нет ли какой ошибки в условии?

[Pripyat]

Спасибо за ответы. Ну значит, действительно, ответ - нет решений.
Условие верно записано - перепроверил.

[provincialka]

Скорее всего, именно на такое решение авторы и намекали. Это довольно известный прием.

[Markiyan Hirnyk]

Рассматриваемая система имеет комплексные решения. Одно из них следующее

$ x=-1/4+i/4\sqrt {11}+1/4\,\sqrt {6-2\,i\sqrt {11}},y=-1/4+i/4 \sqrt {11}+1/4\,\sqrt {6-2\,i\sqrt {11}},z=-1/4+i/4\sqrt {11}+ 1/4\,\sqrt {6-2\,i\sqrt {11}}. $
Еще три решения представляются через корни уравнения четвертой степени. Также имеются решения, представимые через корни уравнения cтепени 60.