Таблицу можно и не запоминать.
Это так называемые дифференциальные уравнения со специальной правой частью. В правой части у них - квазиполином (или их сумма). Квазиполином имеет следующий вид:
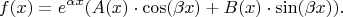

,

здесь - полиномы.
Если правая часть уравнения имеет такой вид, то и частное решение будет иметь почти такой же вид, а именно

Здесь

и

- те же самые числа, что и в

.

и

- полинмы с неопределёнными коэффициентами, имеющие степень, равную максимальной степени полиномов

и

. Например, если

,
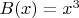
, то

и

будут иметь степень 3.
Число

равно нулю, если число

не совпадает ни с одним из корней характеристического уравнения, которое вы решали в самом начале. То есть в вашем случае если

не равно

,

или

, то

будет равно нулю. Если же совпадение есть, то число

равно числу повторений (кратности) этого корня. Например, если

, то за

вы берёте

, потмоу что

у вас повторяется два раза.
Фактически нужно всего лишь подобрать числа и полиномы в записи для

, чтобы она совпала с данным вам в уравнении

.
Пример. Рассмотрим ваше уранвение в "укороченном" виде. пусть, например, это будет уравнение

Правая часть, очевидно, является квазиполиномом:
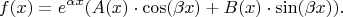
Попробуем подобрать коэффициенты. очевидно, что

. Синусов и косинусов у нас нет. Как можно этого добиться, выбирая

? Например, при

у нас

а

То есть, если мы подставим теперь

и

в выражение

, то получим

Чему должен равняться полином

, чтобы получилась данная нам в уравнении правая часть? Очевидно, что

. А чему должен равняться

? В принципе чему угодно. Для простоты мы можем положить, что

.
Таким образом, мы получили следующее:

Мы знаем, что частное решение должно иметь следующий вид:

Мы знаем

и

, но не знаем

,

и

. Начнём с

. Составим число

. Был ли у нас такой корень характеристического уравнения? Был. Какова была его кратность? Два. Значит,

.
Осталось определиться с

и

. Для этого посмотрим на полиномы

и

. Степень полинома

равна 1 (так как

в первой степени). Очевидно, что степень

больше степени

(вообще, считается, что ноль - эт ополином в степени минус бесконечность).
Таким образом, если старшая степень равна

, то

и

будут полиномами с неопределёнными коэффициентами степени 1, а именно

(Если нужна большая степень, то добавляем слагаемые
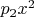
,

и так далее).
В данном случае

в записи частного решения участвовать не будет, так как умножается на

. Частное решение, таким образом, будет иметь следующий вид:

Подставив его в данное уравнение, можно определить, чему равны

и

.
По такой же схеме можно разобрать и все остальные слагаемые в правой части. Причём можно решить рассматриваемое уравнение "по кусочкам" - то есть сначала с первым слагаемым в правой части, потом со вторым, потом с третьим и так далее, сложить все полученные решения и окажется, что эта сумма будет частным решение всего исходного уравнения.
Если потренироваться в решении 5-10 уравнений по такой схеме, Вы их будете щёлкать как орешки. И фактически всё, что нужно знать, - это две формулы для

и

(которые почти совпадают).