Есть массив отсчётов, последовательность вещественных чисел

, ему соответствует массив времён

, нужно эти отсчёты как-то сгладить. Один из способов состоит в следующем: нарисуем пары точек

на координатной плоскости

, рассмотрим их как как точки на графике некоторой (неизвестной нам) функции
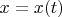
, соединим эти точки последовательно ломаной (то есть просто берётся кусочно линейная интерполяция). за пределы отрезка
![$[t_0, t_n]$ $[t_0, t_n]$](https://dxdy-02.korotkov.co.uk/f/9/2/9/929b4591b7a4f6b8c3e0820cd2bd4c1082.png)
продолжим функцию константами: влево константой

, вправо

. Получившуюся кусочно-линейную функцию обозначим через

. Получившийся график не очень красив, хочется его сгладить, для этого зададимся некоторым числом

, и определим функцию:

Задача состоит в том, чтобы (эффективно) посчитать массив значений

.
Наивный алгоритм имеет асимптотику

, если немного улучшить его бинарным поиском, можно добиться асимптотики

.
Набросок решения за

.
Положим

.
Рассмотрим интеграл кусочно-линейной функции по некоторому отрезку
![$[a, b]$ $[a, b]$](https://dxdy-04.korotkov.co.uk/f/b/d/4/bd4455e79810acc06e3d31c60fb8bfb282.png)
, интеграл это площадь под графиком, значит это сумма площадей трапеций. Он распадается на две части, первая - между двумя точками из сетки

, и два маленьких кусочка по краям (первая часть это часть между крайними точками сетки, которые попадают в отрезок).
Интеграл по двум маленьким кусочкам считается за

, а интеграл между узлами сетки можно подсчитать за

, если предподсчитать кумулятивные суммы

, тогда интеграл между узлами сетки

выразится как

(могу написать выкладку, как это получилось, подробно, если кратко - это получится, если в выражении для интеграла привести подобные члены по

).
Массив кумулятивных сумм считается за один проход, то есть

, потом за второй проход считаем интеграл.
Пока не ясен один момент - как определять

и

для данных

, если делать это бинарным поиском, то итоговая асимптотика получится

. Скорее всего их можно определять адаптивно, используя информацию на предыдущих шагах, но я пока не придумал, как именно.
Вопрос - можно ли решить эту задачу за

? И как её правильно решать? Если пытаться закодить вышеописанный алгоритм, получается какой-то монстр (походу я слишком криво его реализую). Возможно я изобретаю велосипед, и эта задача имеет решение каким-нибудь известным алгоритмом.



