Спасибо. Всё посмотрел. Очень хорошо. В человеческий вид свою конструкцию привёл.
У меня запросили док-во. В общем-то, когда придумываются подобные конструкции, мыслительно их изобретение примерно совпадает с доказательством. Поэтому не писал. Но напишу теперь. Использовал улучшение от
Xaositect, поскольку ближе всего к моему. При этом не умаляю достоинств предложений
Someone. А также благодарен за альтернативные версии.
Рассмотрим



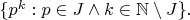
Тогда


есть искомое подсемейство мощности континуум. Действительно, пусть

Тогда, очевидно,

Далее, пусть


Тогда

- противоречие. Значит

и


Про мощность, равную континууму, когда мы имеем перечисление всех элементов булеана счётного мн-ва (кроме пустого мн-ва), я, с Вашего позволения, расписывать не буду.
p.s. Как и обещал, отписался "вечером" - для меня это вечер)



