да, но есть условие

оно мне мешает.

Что тут мешает?
Такие задачи очень удобно решать цепными дробями. Возьмем простой модуль

. Разложим дробь

. Тогда знаменатель "зеркальной" дроби

и есть нужное Вам

:

. Если взять теперь

, то

.


И любое другое по
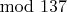
не кратное пяти. Теперь заклюют меня что выложил с потрохами, хотя решения симметричными дробями в учебниках не встречал.