ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ ФЕРМАБудем натуральные числа, которые удовлетворяют уравнению (1),
называть корнями уравнения Ферма и обозначать их

,

,

и


.
Если искать решения уравнения (1) во множестве целых чисел,
то уравнение (1) является диофантовым уравнением Ферма,
решениями которого будут натуральными числа

,

,

и

.
Теорема Ферма гласит: нет таких натуральных чисел

,
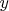
и

,
которые бы при целой степени

удовлетворяли уравнению (1).
Можно считать, что натуральные числа

,
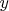
и

являются попарно взаимно простыми числами,
так в противном случае общий множитель можно сократить.
Рассмотрим вещественное уравнение с вещественными переменными

,
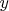
,

и


где
![$ z = \sqrt[n]{x^n+y^n} $ $ z = \sqrt[n]{x^n+y^n} $](https://dxdy-02.korotkov.co.uk/f/1/4/5/1456a7f75666ee992b993fefa8f3389782.png)
;

.
Графики зависимостей

при различных фиксированных значениях

и
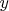
показаны на Рис. 1.
Приведенные графики показывают, что при фиксированных значениях

и
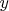
функции

являются однозначными и монотонно убывающими.

Очевидно, что при

корни уравнения Ферма являются и корнями уравнения (2).
Следует заметить, что при

других корней уравнение (2) не имеет,
то есть множества корней диофантова уравнения Ферма и уравнения (2) совпадают,
то есть уравнение (2) и диофантово уравнение Ферма эквивалентны при

.
Рассмотрим непрерывную и гладкую вещественную функцию
вещественных переменных

,

,

и

(левая часть уравнения (2)).

где
![$ z = \sqrt[n]{x^n+y^n} $ $ z = \sqrt[n]{x^n+y^n} $](https://dxdy-02.korotkov.co.uk/f/1/4/5/1456a7f75666ee992b993fefa8f3389782.png)
;

;

и

- достаточно малое число.
Функция (3) непрерывная и гладкая, имеющая непрерывные производные всех порядков и
имеющая непрерывные производные на всем множестве определения.
Очевидно, что при

корни уравнения Ферма обращают функцию (3) в ноль,
то есть в этих точках функция (3) имеет локальные минимумы.
Таким образом, задачу решения диофантового уравнения Ферма (1) свели к решению
тригонометрического уравнения (2) и задаче нахождения экстремумов функции (3)
при

.
Очевидно, что при

и целых

,
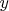
,

и

функция

.
Так же очевидно, что при

и целых

,
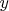
,

и

функция

.
Запишем необходимые условия существования экстремума функции (3):


где
![$ z = \sqrt[n]{x^n+y^n} $ $ z = \sqrt[n]{x^n+y^n} $](https://dxdy-02.korotkov.co.uk/f/1/4/5/1456a7f75666ee992b993fefa8f3389782.png)
или

.
Так как в три уравнения (4), (5) и (6) входят пять переменных, то три переменные будут независимыми
(их значения можно задавать произвольно), а две зависимыми (их значения определяются из полученной
системы уравнений). Поскольку между переменными

и

имеет место однозначная зависимость,
то из пяти переменных

,
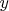
,

,

и

в качестве независимых можно принять

,
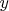
,

,
а переменные

и

считать зависимыми.
Будем искать координаты минимума функции (3) во множестве целых координат,
поэтому запишем необходимые условия существования экстремума функции (3) в точках
с целыми координатами

,

и

, для чего фиксированные координаты

,

и

произвольной точки подставим в уравнения (4), (5) и (6).
Тогда получим следующую систему уравнений


где
![$ z_0 = \sqrt[n]{x_0^n+y_0^n} $ $ z_0 = \sqrt[n]{x_0^n+y_0^n} $](https://dxdy-04.korotkov.co.uk/f/3/2/d/32d29d1dae4fd8f60ce788700d631aeb82.png)
или

,
здесь

определяется из уравнений (9).
Таким образом, получили два уравнения (7) и (8) с переменными

и

и
постоянными коэффициентами

,

и

.
Перепишем уравнения (7) и (8) в следующем виде


.
Следует заметить, что уравнения (10) и (11) являются необходимыми условиями существования экстремума функции (3).
Любое уравнение с двумя переменными вида

можно считать заданием неявной функции

.
Поэтому уравнения (10) и (11) можно рассматривать как неявные функции
переменной

от переменной

, то есть как функции

.
Таким образом, уравнения (10) и (11) позволяют найти две функции

, в которых
коофициенты

,

и

постоянны и не зависят от переменной

.
Выразим из уравнений (10) и (11) функции

в явном виде:

,

.
Предположим, что диофантово уравнение Ферма имеет решение

,

,

и

.
Графики функций (12) и (13) при различных

,

и

показаны на рис. 2.

Функции (12) и (13) это неявные функции, полученные в явном виде из уравнений (10) и (11),
которые являются необходимыми условиями существования экстремумов функции (3).
Функции (12) и (13) непрерывные и гладкие в окрестности точки

,
а в самой точке

функции не определены.
Функция (3) может иметь экстремумы не при любых целых координатах

,

и

,
а только когда координаты

,

и

.
Этим и обусловлен тот факт, что функции (12) и (13) не определенны в точке

.
Функции (12) и (13) в точке

не определены, так как в числителе дробей при

имеют место неопределенности типа 0/0 .
Раскроем неопределенности по правилу Лопиталя и найдем пределы функций (12) и (13) когда

.
Эти пределы равны

.
Пределы функций (12) и (13)

не зависяn от значений

,

и

и равны 2,
то есть

при любых значениях

,

и

.
Функции (12) и (13) в точке

имеют разрыв I-го рода, который может быть устранен. Поскольку функции (12) и (13) имеют
пределы

при

,
то функции (12) и (13) могут быть превращены в непрерывные и гладкие
на всем множестве их определения, если их в точке

до определить
их пределами

.
Производные функций (12) и (13) по переменной

определяются следующими функциями

,

.
Очень важно, что в точке

производные функций (14) и (15) по

не определенны,
но имеют пределы равные нулю, то есть в точке

производные

.
Это подтверждает, что функции (12) и (13), до определенные при

значениями

,
будут и гладкими.
Предположим, что диофантово уравнение Ферма имеет целочисленное решение

,

,

и

,
тогда функция (3) в этих точках обращается в ноль, а поэтому в этих точках она имеет минимумы.
Поскольку функции (12) и (13) справедливы при целых значениях

,

и

,
то они будут справедливы и при

,

,

и

.
Поэтому функции (12) и (13) могут переписаны в виде

,

.
Следует заметить, что функции (16) и (17) не определены при

, но достоверно известно,
что при

в точках с координатами

,

,

и

имеют место экстремумы,
поэтому функции (16) и (17) должны быть до определены значениями

при

.
На Рис. 2. показано до определение функций (12), (13), (17) и (17) значениями

и

.
Координаты точек экстремумов функции (3) могут быть найдены, как точки
пересечения до определенных функций (16) и (17), что дает координаты

и

для точки экстремума функции (3).
Графическое решение системы уравнений (10) и (11) проиллюстрировано на Рис. 2. ,
где координата

экстремума функции (3) находится как точка пересечения
до определенных функций (16) и (17).
Следует заметить, что если до определить функции (16) и (17) значением

,
то функции (16) и (17) будут непрерывными и гладкими,
а если функции (16) и (17) до определить значением

, то функции (16) и (17)
будут иметь разрыв при

.
Для того, чтобы установить, может ли функция (3) иметь минимумы при том или ином значении

надо воспользоваться свойствами непрерывных и гладких функций, для которых функции (16) и (17),
получаемые из необходимых условий существования экстремума (10) и (11), непрерывны.
Непрерывные и гладкие функции обладают следующими свойствами:
1. В области определения эти функции не только непрерывны сами, но непрерывны и их производные по координатам;
2. При непрерывном изменении переменных координаты экстремумов непрерывных и гладких функций непрерывным
образом изменяются, а сами экстремумы функций смещаются в пространстве;
3. При непрерывном изменении переменных координаты экстремумов непрерывных и гладких функций не должны
иметь разрывов».
4. Для непрерывных и гладких функций, функции, получаемые из необходимых условий существования
экстремума, непрерывны.
Если функция (3) имеет минимумы в точках

,

,

и

при

, то функция (3) будет иметь минимумы и в точках

,

,

и

при любых значениях

, причем при непрерывном изменении

координаты точек минимумов
изменяются непрерывным образом.
Из свойств непрерывных и гладких функций следует, что функции (16) и (17) должны быть непрерывными,
поэтому функция (3) может иметь минимумы только при

,
а при других значениях

функция (3) минимумов не имеет.
Таким образом получили, что при

непрерывность функций (16) и (17) не нарушается , а при

нарушается непрерывность функций (16) и (17).
Поскольку функция (3) не имеет минимума при

,
то и диофантово уравнение Ферма не имеет целочисленных решений при

.
Таким образом доказали, что при

диофанотово уравнение Ферма не имеет целочисленных решений.
Следует заметить, что доказательство теоремы Ферма выполнено методом, основанном
на сведении решения диофантового уравнения Ферма к решению
эквивалентного тригонометрического уравнения, нахождению минимумов функции,
получаемой из тригонометрического уравнения и использовании свойств экстремумов
непрерывных и гладких функций. Метод не позволяет находить решения диофанотовых уравнений,
но в ряде случаев позволяет установить, когда диофантово уравнение не имеет решений.