Как известно, мощность статистического критерия, представляет собой вероятность верного принятия альтернативной гипотезы. Применительно к коэффициенту корреляции

.
Как правило, проверяется только нулевая гипотеза. Каким образом в таких условиях можно оценить ошибки второго рода, не совсем понятно. Хотя очевидно, что задаваемому уровню значимости

всегда соответствует вполне определённая мощность

. Причём, по мере уменьшения

,

так же уменьшается, т.е. с увеличением специфичности, чувствительность теста всегда падает. Возникает справедливый вопрос о выборе оптимального соотношения

и

.
Особенно остро он встаёт, например, при отборе признаков. Моя личная практика показывает, что при этом, наилучшие результаты получаются при
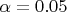
, хотя теоретического обоснования этому никакого у меня нет. О мощности коэффициента корреляции информации нигде найти не удаётся, за исключением, пожалуй того, что корреляция Пирсона мощнее ранговых корреляций.
Интуиция показывает, что для нахождения мощности необходимо оценить вероятность сложной альтернативной гипотезы

, но как это сделать, я к сожалению не знаю. Но, по крайней мере для корреляций Пирсона, это видимо возможно. Так как известны законы распределения вероятностей для любых её значений.
Буду рад любой помощи по данному вопросу. В частности - ссылкам на полезную литературу, или другую информацию. А так же другим полезным советам.



