Два игрока по очереди ставят точки в клетки таблицы
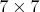
. За один ход
ставится ровно одна точка. В одну клетку может быть поставлено несколько
точек (ставить точки на границы клеток нельзя). Проигрывает тот, после
чьего хода в клетках какой-то строки или столбца суммарно будут стоять 5
точек. Кто из игроков может обеспечить себе победу независимо от игры
соперника?
(Минская городская олимпиада)............................................................
Меня смущает, что
в одну клетку может быть поставлено несколько точек, ведь добавление данной детали в условие задачи лишь облегчает её решение!
Действительно, вторму игроку для победы достаточно в ответ на ход первого игрока ставить точку в той же самой клетке, что и первый. Изначально таблица пуста (во всяком случае, в условии не указано, что это не так), следовательно, в каждом строке и в каждой столбце чётное число точек. Ход первого игрока нарушает условие чётности (ровно в одной строке и ровно в одном столбце теперь нечётное число точек), а ответный ход второго возвращает всё на круги своя - и снова в каждой строке и в каждом столбце чётное число. Следовательно, первый игрок рано или поздно проиграет.
Разве не так?
А если изменить условие и запретить ставить в одну клетку более одной точки, что тогда?
Пожалуйста, помогите решить.
Заранее благодарю!



