Имеется интегральчик

Соответственно применяю вот такие замены:

После всех упрощений интеграл сводится к такому:

Знаменатель имеет два полюса второго порядка, из которых внутри контура лежит только один, а именно:
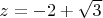
Далее у меня начинается путаница в голове, по сути для вычета высших порядков есть всем известная общая формула, но меня смущает то, что расчет разрастается весьма прилично, запутаться как пить дать можно, отсюда вопрос правильно-ли я поступаю вообще, получается что производную

надо искать от выражения

как-то не очень весело.. если найти производную то там еще менее весело :( Вообще не уверен что правильно поступаю