Задача по оптимизации

[likusta]

Здравствуйте!
Нам задали задачу: $\int\limits_0^{+\infty} e^{-2t} (-\frac{u^2}{2}+xu-\frac{x^2}{2})dt \rightarrow max, x'=u,x(0)=x_0>0.$
Покажите, что $x,m$ удовлетворяют системе уравнений: $x'=x+m$, $m'=m$.
Нам не рассказали, что такое $m$, поэтому не совсем понятно, как это решать. Скажите, пожалуйста, правильно ли я понимаю, что тут под $m$ обычно подразумевается $m=\psi e^{2t},$ которое получается(точнее такое обозначение просто вводится) в ходе применения принципа максимума Понтрягина. Если это так, то первое уравнение у меня не вышло, а вместо второго получилось $\dot m = 2m$. Получилось оно так:
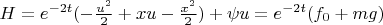
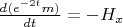
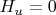
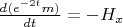
$H=e^{-2t} (-\frac{u^2}{2}+xu-\frac{x^2}{2})+\psi u = e^{-2t}(f_0+mg)$, где $m=e^{2t}\psi$. Потом составил $\dot \psi = -H_x$, получилось, $\frac{d(e^{-2t}m)}{dt}=-H_x$, воспользовался необходимым условием экстремума $H_u=0$ получилось, что $x=u$, подставил это в $\frac{d(e^{-2t}m)}{dt}=-H_x$ и получилось, что $\dot m - 2m =0$.

[likusta]

Спасибо, если кто-то подумал об этом. У меня получилось решить, сделал один ложный вывод и поэтому получилась ошибка.