Ну, собственно, для матрицы 100х100 степенной метод имеет одно достоинство - программировать его не просто, а очень просто. Хотя и тут можно нарваться.
Помнится, один мой знакомый слишком буквально понял правило расчёта
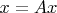
и, вычислив очередной элемент вектора, его сразу же помещал на место. И долго недоумевал.
Скорость сходимости - да, может быть прискорбно низкой. И даже никакой Заратустра не запретил максимальному С.З. быть кратным. Хотя для некоторых матриц можно доказать факт отсутствия кратности и получить оценки скорости сходимости.
(Оффтоп)
Задача о рейтинге футбольных команд - матрица A содержит встреч команд меж собой, для расчёта рейтинга принимается, что победа над сильной командой даёт больший вклад в рейтинг, задача сводится к

, и поскольку матрица A неразложима и имеет положительные элементы, по теореме Фробениуса-Перрона у неё одно максимальное действительное С.З.
А при кратном С.З. собственный вектор в ходе вычислений вправе прыгать как угодно в пространстве, натянутом на соответствующие кратному значению собственные вектора.
Для борьбы с этим в рамках степенного метода придумали одновременные итерации, когда берётся набор k ортогональных (для начала - можно просто случайных) векторов, их умножают на матрицу, полученные вектора ортогонализуют и запускают в цикл по новой. Работает, но не панацея. Скорость определяется отношением первого и (k+1) С.З., и тоже может быть невысока.
Степенной метод и иже с ним не для доступной обычным образом матрицы, они для случая, когда матрица очень велика и разрежена, или велика и хранима во внешней памяти, или велика и её элементы не хранятся, а вычисляются по требованию, в общем, когда единственная доступная операция это умножить вектор на эту матрицу. Да и там степенной метод и его продвинутые версии не единственный вариант, но, по крайней мере, "препарат выбора".
Хотя лично я испытываю нежные чувства к методу Якоби (вращений), но в данном случае его рекомендовать бы не стал. Его главное достоинство - гарантированная ортогональность всех собственных векторов - здесь явно излишне, да и "покупать корову ради одного бифштекса" в смысле считать все собственные значения и вектора, когда требуется одно минимальное - "половое излишество, паркетный пол линолеумом покрывать".
Мне кажется, тут лучше QR найти трудно. Правда, программируется он двухэтапно. Сперва надо привести (отражениями) к трёхдиагональной форме, а уж потом QR. Причём без сдвигов сразу будет находиться наименьшее С.З.
(Оффтоп)
Силами студентов в подшефном колхозе был построен Q-рятник на 1024 QRместа
Или можно, также приведя к трёхдиагональному виду, использовать бисекции.



