Можете отправить в точное место какого либо учебника чтоб увидеть математическое выражение, которое описывает статическое поле виртуальными фотонами?
Математическим выражением для электростатического поля точечного заряда служит кулоновский потенциал, определяющий энергию взаимодействия двух зарядов. Как известно, эта энергия зависит от расстояния
между взаимодействующими зарядами пропорционально
(в вакууме, где нет никаких эффектов экранирования наших двух зарядов ещё какими-либо частицами).
Квантовая теория даёт такое же математическое выражение для энергии электростатического взаимодействия двух зарядов (в вакууме, на расстояниях
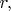
значительно превышающих комптоновскую длину волны любых заряженных частиц, способных вызвать поляризацию вакуума). При этом оказывается, что этому же выражению пропорциональна "амплитуда вероятности распространения виртуального фотона" между двумя статическими зарядами. Сей факт выводится в учебниках по квантовой теории поля (КТП), в них амплитуда вероятности перехода фотона с места на место называется
пропагатором фотона.
Однако, не думайте, что сей сюжет прост как дважды два. Объяснить всё парой фраз и одной формулкой не получится (см., например, такой учебник, как ЛЛ-4 "Квантовая электродинамика": понятия "пропагатор" и "виртуальный фотон" там впервые вводятся в § 73; в § 75 есть немногословное, но принципиально важное пояснение: <<
Введённое в предыдущих параграфах понятие о функциях распространения (пропагаторах) играет основную роль в аппарате квантовой электродинамики. Фотонный пропагатор становится основной величиной, характеризующей взаимодействие двух электронов.>> Вывод формул для фотонного пропагатора см. в § 76, в частности, см. формулу (76,16)). Кратко говоря, в импульсном представлении фотонный пропагатор при
ведёт себя как
поэтому его выражение в координатном представлении (получаемое преобразованием Фурье) оказывается как раз "кулоновским потенциалом"
В деталях всё это удастся усвоить только при наличии серьёзной подготовки. К нашему счастью, Ричард Фейнман саму идею о том, что взаимодействия можно в квантовой теории описывать через обмен виртуальными частицами, сумел мастерски изложить в своих замечательных Лекциях по Физике, адресованных начинающим физикам. Смотрите в ФЛФ: выпуск 8 "Квантовая механика (I)", глава 8, § 1 "Молекулярный ион водорода" и § 2 "Ядерные силы".
Конечно, столь серьёзная идея, притом квантово-механическая, там тоже не парой фраз разъясняется; Фейнман ведёт читателя к ней плавно, причём от читателя требуется высокий уровень вдумчивости. Логика там вот какая.
Сначала в задаче об энергии химической связи протона с атомом водорода выводится, что эта энергия пропорциональна амплитуде перехода электрона с места на место сквозь потенциальный барьер между двумя протонами. Этот факт позволяет ввести представление о "виртуальном состоянии" электрона и идею о том, что химическую связь между атомами можно понимать как результат обмена таким "виртуальным" электроном.
Затем по аналогии рассматривается ядерное взаимодействие между протоном и нейтроном за счёт обмена виртуальным мезоном (модель Юкавы): в этом сюжете выясняется, что потенциал Юкавы пропорционален амплитуде перехода виртуального мезона.
И, как очередное звено в этой цепочке аналогий:
Фейнман писал(а):
С точки зрения "частиц" кулоновское взаимодействие между двумя электронами
вытекает из обмена виртуальными фотонами. ... виртуальный обмен фотоном приводит к энергии взаимодействия, которая меняется просто обратно пропорционально
— в точности как нормальная кулоновская потенциальная энергия! В "частичной" (от слова частица) теории электромагнетизма процесс обмена виртуальным фотоном приводит ко всем явлениям электростатики.
Более подробно, на языке формул, объяснение кулоновского взаимодействия в терминах обмена виртуальными фотонами Фейнман привёл в книге "Теория фундаментальных процессов"; см. там стр. 108-113.
(цитата из раздела ВИРТУАЛЬНЫЕ И РЕАЛЬНЫЕ ФОТОНЫ)
![$$\vec E=\frac{e\left(1-\frac{v^2}{c^2}\right)}{\left(R-\frac{\vec v\vec R}c\right)^3}\left(\vec R-\frac Rc\vec v\right)+\frac e{c^2\left(R-\frac{\vec v\vec R}c\right)^3}\left[\vec R\times\left[\left(\vec R-\frac Rc\vec v\right)\times\dot{\vec v}\right]\right]\text{,}$$](https://dxdy-04.korotkov.co.uk/f/f/5/e/f5e9e6891eb5650e4fe140ed56bc7d8382.png "$$\vec E=\frac{e\left(1-\frac{v^2}{c^2}\right)}{\left(R-\frac{\vec v\vec R}c\right)^3}\left(\vec R-\frac Rc\vec v\right)+\frac e{c^2\left(R-\frac{\vec v\vec R}c\right)^3}\left[\vec R\times\left[\left(\vec R-\frac Rc\vec v\right)\times\dot{\vec v}\right]\right]\text{,}$$")
![$$\vec H=\frac 1R[\vec R\times\vec E]\text{,}$$](https://dxdy-03.korotkov.co.uk/f/e/1/d/e1d2798b583a277604d41575f1cefe4e82.png "$$\vec H=\frac 1R[\vec R\times\vec E]\text{,}$$")
. Второй же член представляет собой поперечное поле, убывающее как 
и представляющее собой поле некоторой электромагнитной волны, и это слагаемое он называет далее излучением заряда. Далее он отмечает, что это определение шире обычного определения электромагнитного излучения, которое определяется в волновой зоне, и что поле, описываемое вторым членом, вообще говоря, не является полем электромагнитного излучения, распространяющегося со скоростью света.
