вроде внимательно посмотрел условие стационарности

отсюда

Ах, вот в чём дело. Ну да, у Вас были причины так подумать.
Обозначим

. Мы требуем, чтобы для подвижной правой границы выполнялось условие
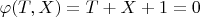
. При этом

является функцией

. В такой ситуации есть две разные производные

по

:

частная производная

: Вы считаете

и

независимыми переменными, и находите производную по

при постоянном

;
 полная производная
полная производная 
: Вы учитываете и непрямую зависимость

от

— через

.
Полная производная связана с частной так:
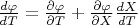
В вариационном исчислении встречаются и частная, и полная производная.
В Вашем случае по контексту требовалась частная производная по

, Вы нашли полную.