Нас например в университете учили тупо заучивать таблицу первообразных, свято веря в неё,
Позвольте не поверить. Ну, то есть в то, что требовали учить наизусть, вполне верится - это навык, избавляющий от труда беспрестанно заглядывать в справочник. А что требовали "свято верить", не смея усомниться - не верю. Никто не мешал перестать верить и проверить. Продифференцировав.
Конкретно непонятно куда деваются все члены, начиная с 3-го в разложении по биному. Ими пренебрегают, оставляя только член, не содержащий множителей степеней
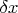
?
Вполне возможно, что Ньютон, Лейбниц и прочие в их время именно так и поступали. Отбрасывая "члены второго и большего порядка малости". Что при их гениальной интуиции к ошибкам не приводило, но потом обнаружились некоторые парадоксы от такого вольного обращения. Пришёл Коши и сделал кошерно - через понятие предела, устранив парадоксы наподобие тех, над которыми издевался епископ Беркли. Сейчас следуют пути, указанному Коши и на парадоксы не натыкаются.