Прошу простить мою наивность, но интересует вопрос: откуда Лейбниц и Ньютон взяли, что первообразная от


?
Можно ли это как-то вывести? Например у меня получается другая формула для первообразной, следующая из моих философских соображений, в которых я сомневаюсь и которые не хотел бы излагать до ознакомления с результатами и рассуждениями Ньютона и Лейбница. Нас например в университете учили тупо заучивать таблицу первообразных, свято веря в неё, поэтому попыток решения не привожу, а привожу лишь готовую формулу в которой посмел усомниться.
Попытки решения таковы: первообразная

функции

- это такая функция, производная которой

. Здесь всё формально верно. Но, дифференциальное и интегральное исчисления разрабатывались согласованно и не имеют противоречий друг с другом. Поэтому, чтобы удостовериться в справедливости формулы для первообразной степенной функции, возникает необходимость обосновать формулу для производной степенной функции, причем обосновать не с помощью первообразной, а как-то иначе. Например я знаю определение производной: Производная функции - предел отношения приращения функции к приращению аргумента при приращении аргумента стремящемся к нулю. Возникают трудности с пониманием того, как с помощью этого определения вывести формулу для производной степенной функции?

раскроем скобки в соответствии с биномом Ньютона:

Не соображу что делать дальше, чтобы получить необходимую формулу для производной.
Конкретно непонятно куда деваются все члены, начиная с 3-го в разложении по биному. Ими пренебрегают, оставляя только член, не содержащий множителей степеней
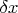
? И еще непонятно почему у меня получился минус. Да, минус у меня получился из-за неправильной формулфы , определяющей производную, нужно поменять вычитаемое и уменьшаемое местами:

, тогда в итоге получим:

Остался один вопрос: что происходит со всеми членами, начиная со второго? Пренебрегаем ими в силу их малости, т.к. они содержат множитель
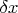
, стремящийся к нулю?
В зависимости от ответа на него могут еще появиться другие вопросы.