Среди задач (как я понял, не решённых) одного семинара трёхлетней давности я нашёл одну особо меня заинтересовавшую: доказать, что множество квадратичных вычетов в простом поле

не представимо в виде

для

.
Я решил попробовать подступиться к ней от противного для самого простого случая

, то есть попробовать представить как можно большее подмножество квадратичных вычетов в виде

. Тут-то всё и началось.
Я взялся на компьютере посчитать

, где

- множество квадратичных вычетов.
Для простых вида

значения

оказались независимыми от

, а для
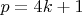
значения

незначительно (но не на константу) больше для

, являющихся квадратичными вычетами. Ну да это ладно, я не понимаю, почему это именно так, но ясно, что это связано с (не)квадратичностью

. Впрочем, почему для
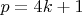
все значения

одинаквые - не понимаю. Если это очевидно, пожалуйста, объясните.
Главное другое - я, естественно, стал считать, чему же равно это самое

для разных

. Нащупать точные формулы для них через какие-то рациональные выражения не получилось, зато однозначно видно, что

при

(и этот факт стал основным поводом для открытия этой темы), причём стремление очень быстрое, чуть ли не по гиперболе. Есть ещё один забавный факт - для простых вида

значения

монотонно убывают (проверял до

, чуть больше чем

простых), и то же самое для простых вида

. Но для всего множества

график

бесконечно колеблеться то вверх то вниз (в смысле "производной", если можно так выразиться).
Буду благодарен за любые материалы по этой теме и рад желающим поисследовать это вместе со мной. Есть ещё много идей для экспериментов, и подозрительных закономерностей при малых

, которые хочется проверить для больших, но хотелось бы для начала выяснить, не изучена ли уже эта область, и не лежат ли все эти вопросы где-то на поверхности, где я их просто не вижу.



