Выбор системы координат для численного решения ОДУ на сфере

[Legioner93]

Есть уравнение, описывающее эволюцию единичного вектора. Это уравнение хочется численно решать.

$$\mathbf{\dot{r}} = \mathbf{r} \times \mathbf{f(r)}$$

Само уравнение устроено так, что вектор $\mathbf{r}$ всегда остаётся на сфере, поскольку $d\mathbf{r} \cdot \mathbf{r} \equiv 0$

Однако, классические явные методы численного интегрирования, например метод Эйлера 1-го порядка, или метод Рунге-Кутта 4-го порядка, если их применять "влоб", этим свойством уже не обладают.
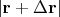
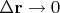
Конечно, прирост длины $|\mathbf{r} + \Delta\mathbf{r}|$ имеет второй порядок малости, но ошибка всё равно постепенно набегает, и это плохо. Сейчас для решения этой проблемы я поступаю так: в конце каждого шага я принудительно возвращаю вектор на сферу, то есть нормирую его. Это работает в пределе по $\Delta\mathbf{r} \to 0$, но суровая реальность заставляет решать это уравнение для, скажем, $|\Delta\mathbf{r}| \sim 0.5$.

Возникла идея переписать исходное уравнение так, чтобы сфера cтала для него "родной", тогда численные методы хоть и будут давать ошибку при увеличении шага, но хотя бы не будут выбрасывать вектор со сферы. За счёт этого предполагается увеличить максимально возможный шаг численного интегрирования.

Сразу хочется переписать уравнение в фиксированной сферической с.к., и сделать это легко. Однако, сферическая с.к. не подходит, потому что имеет неустранимые особенности в полюсах (а вектор $\mathbf{r}$ будет переходить через полюса любой заранее выбранной сферической с.к.).
Можно выбирать "плавающую" сферическую с.к., отсчитывая зенитный угол от $\mathbf{f(r)}$. Это плодотворная идея, у нас люди этим занимаются, и возможно я в итоге сделаю так же. Однако там много своих сложностей.

Вопрос состоит в том: а есть ли другие пути? Я уже понял, что двумерной фиксированной с.к. не обойтись, там всегда будут особые точки (Википедия говорит, что здесь работает теорема о причёсывании ежа). А если разрешить три координаты, или даже четыре? Можно ли что-то придумать?

Что я ещё попробовал: направляющие углы (арккосинус от декартовых компонент вектора).
Однако численная особенность всё равно остаётся, потому что если

$$r_x = \cos \alpha_x, \qquad \dot{r_x} = - \sin \alpha_x \dot{\alpha_x},$$

то для того же метода Эйлера получаем

$$\Delta\alpha_x = \Delta t \frac{f_y \cos \alpha_z - f_z \cos \alpha_y}{\sin \alpha_x}$$

И вот этот синус в знаменателе всё портит.

В общем, что известно про численное решение таких уравнений? За ссылки на литературу тоже буду благодарен. Насколько я понимаю, корень проблемы здесь в том, что исходное уравнение записано в трёхмерной (декартовой с.к.), хотя его пространство решений существенно двумерное.

[arseniiv]

Legioner93 в сообщении #1256382 писал(а):

Возникла идея переписать исходное уравнение так, чтобы сфера cтала для него "родной", тогда численные методы хоть и будут давать ошибку при увеличении шага, но хотя бы не будут выбрасывать вектор со сферы. За счёт этого предполагается увеличить максимально возможный шаг численного интегрирования.

Сразу хочется переписать уравнение в фиксированной сферической с.к.

Одно с другим не очень связано. Просто надо обобщить тот же метод Эйлера на многообразия. Вместо сложения появится, видимо, перенос по геодезической (в данном случае по большому кругу). Так что можете попробовать вращать точку сферы вместо переноса и нормирования. Ну или я пишу бред, потому что этим ни разу не занимался.

[Legioner93]

arseniiv в сообщении #1256383 писал(а):

Просто надо обобщить тот же метод Эйлера на многообразия.

Ну а как это сделать, кроме как ввести координаты на многообразии? Про координаты я уже расписал выше, всё что знаю.

[pogulyat_vyshel]

ну может этот вектор просто тупо нормировать на каждом шаге

[arseniiv]

Legioner93 в сообщении #1256388 писал(а):

Ну а как это сделать, кроме как ввести координаты на многообразии? Про координаты я уже расписал выше, всё что знаю.

Так не в координатах же дело, многообразие никуда не денется, есть они или нет. Главное отличие в том, что мы делаем только то, что допустимо для многообразия, то есть вместо итерации $\Delta\mathbf r = \mathbf r + (\mathbf r\times\mathbf f(\mathbf r))\Delta t$ в методе Эйлера должен быть, скажем, перенос $\mathbf r$ по большому кругу, проходящему через $\mathbf r$ в направлении $\mathbf r\times\mathbf f(\mathbf r)$ на определённую величину, билинейно зависящую от $\Delta t$ и модуля $\mathbf r\times\mathbf f(\mathbf r)$. Это поворот, его можно делать в каких хочется координатах, и проще оставить декартовы координаты пространства, в которое помещена сфера. Поворачивайте как хотите — матрицами, кватернионами.

-- Вт окт 17, 2017 20:29:07 --

Ну и другие методы аналогично исправить, когда это вообще возможно.

[Legioner93]

arseniiv
Да несложно придумать, как сделать один поворот. И сделать его можно хоть в декартовой с.к., вы правы. Проблемы возникают, когда такие повороты надо между собой как-то "складывать", как например в методе Рунге-Кутты-4, или почти любом другом.

Вместо этого я хочу как-нибудь сразу перейти в "родное" для сферы представление, посчитать там самый обычный Рунге-Кутты-4 (или любой другой метод) в новых координатах, а потом вернуться в декартово представление. Это можно сделать, например, в сферических координатах, но тогда возникают трудности на полюсах.

-- Вт окт 17, 2017 19:23:08 --

pogulyat_vyshel в сообщении #1256391 писал(а):

ну может этот вектор просто тупо нормировать на каждом шаге

Об этом есть в стартовом посте

[pogulyat_vyshel]

Если говорить серьезно, то квалифицированные люди сперва проводят качественный анализ системы, а уж потом суют ее в компьютер и считают не все подряд, а только те решения и фрагменты фазового потока, о которых нужна количественная информация. Автономная система на двумерной сфере это штука в любом случае не сложная и вполне поддающаяся анализу. Ну а уж когда будете понимать как устроен поток, тогда сообразите и как сферическую систему координат вводить. А может это уже и не понадобится

-- 17.10.2017, 20:55 --

Ведь вы же какие-то смешные вещи пишите:

Legioner93 в сообщении #1256382 писал(а):

Однако, сферическая с.к. не подходит, потому что имеет неустранимые особенности в полюсах (а вектор $\mathbf{r}$ будет переходить через полюса любой заранее выбранной сферической с.к.).

По теореме существования и единственности, через полюса проходит не более двух решений, ну и разберитесь с этими решениями отдельно, а еще лучше введите сферическую систему так, чтоб полюс приходился на положение равновестия

[arseniiv]

Legioner93 в сообщении #1256402 писал(а):

Проблемы возникают, когда такие повороты надо между собой как-то "складывать", как например в методе Рунге-Кутты-4, или почти любом другом.

Ну, тут надо смотреть, конечно, можно ли обобщить это место в методе, и если да, то как. Вообще у методов обычно есть обоснования, вот оттуда и должно быть ясно, зачем делается то и это. Наверно, всё, что можно было здесь обобщить, уже должно было появиться, и остаётся только понять, где про это читать.

[Legioner93]

Цитата:

По теореме существования и единственности, через полюса проходит не более двух решений, ну и разберитесь с этими решениями отдельно

Поясняю: все вычисления на компьютере ведутся с определённой точностью. К тому же, задаётся какой-то конечный шаг интегрирования.
Всё это приводит к тому, что достаточно попасть в некоторую окрестность полюса, где всё становится плохо. На этот счёт у вас тоже есть какая-нибудь теорема? Или просто поверите мне, что сферическая с.к. тут работать не будет?

[arseniiv]

Сейчас пришло в голову, что вместо нормирования можно «исправлять» по-другому, проецируя на сферу центральной проекцией с центром не в центре сферы (это нормирование), а в диаметрально противоположной точке относительно той, которой равен $\mathbf r$ сейчас. Это должно быть чуть лучше, и к этому можно даже подвести какое-то обоснование в терминах систем координат. (Но всё равно это не по-честному.)

[Someone]

Может быть, взять две-три фиксированные системы координат на сфере, и вести расчёт в одной из них, пока точка не подойдёт к полюсу "слишком" близко. В этот момент перейти в другую систему координат и вести расчёт в ней, пока не подойдём к полюсу "слишком" близко. И так далее.

[pogulyat_vyshel]

(Оффтоп)

а потом придет нормальный математик и за 20 минут выяснит, что в этой системе все траектории сматываются с одного положения равновесия на сфере и наматываются на другое. Ну или что система на сфере первый интеграл имеет Так просто из опыта

[Legioner93]

pogulyat_vyshel

pogulyat_vyshel в сообщении #1256427 писал(а):

а потом придет нормальный математик и за 20 минут выяснит, что в этой системе все траектории сматываются с одного положения равновесия на сфере и наматываются на другое. Ну или что система на сфере первый интеграл имеет Так просто из опыта

Чтобы немного умерить ваше самомнение. "Нормальных математиков" эта индустрия ждёт уже лет 20. Пока не нашла. Если вы один из таких, или знаете такого - пишите в личку, я обещаю публикации в топовых журналах и безбедное существование.

Потому что:
1. Это уравнение из микромагнитного/атомистического моделирования. На самом деле, этих $\mathbf{r}$ целых $N$ штук, где $N$ доходит до миллиона. То есть имеем миллион уравнений.
2. Уравнения не независимы. Правая часть уравнения зависит от всего ансамбля, то есть $\mathbf{\dot{r}}_i = \mathbf{r}_i \times \mathbf{f(r_1, r_2, \dots, r_N)}$
3. Кроме того, в $\mathbf{f(r_1, r_2, \dots, r_N)}$ имеется стохастическое слагаемое (вики про СДУ).

Все эти детали я упустил, потому что не важны для того вопроса, который я задал в стартовом посте! И остальные это поняли. Но дальше в тему ворвались вы, весь такой в белом, и начали рассказывать, что кругом все дураки.

-- Вт окт 17, 2017 21:47:37 --

Someone в сообщении #1256423 писал(а):

Может быть, взять две-три фиксированные системы координат на сфере, и вести расчёт в одной из них, пока точка не подойдёт к полюсу "слишком" близко. В этот момент перейти в другую систему координат и вести расчёт в ней, пока не подойдём к полюсу "слишком" близко. И так далее.

Someone
Хм. Да, возможно что-то подобное сработает.

Или лучше даже так: на каждом шаге будем выбирать полярную с.к., у которой все особенности расположены максимально далеко от $\mathbf{r}$, то есть $\mathbf{r}$ будет на экваторе. Считаем все стадии многостадийного метода (тот же Рунге-Кутты-4, или метод средней точки) в этой с.к., после чего переходим на новый шаг, и там уже будет новая с.к.

Попробую так сделать, спасибо за идею.

[pogulyat_vyshel]

Legioner93 в сообщении #1256382 писал(а):

Есть уравнение, описывающее эволюцию единичного вектора. Это уравнение хочется численно решать.

$$\mathbf{\dot{r}} = \mathbf{r} \times \mathbf{f(r)}$$

При заданном начальном условии $\mathbf{r}(t=0)=\mathbf{r}_0$ можно вместо исходной системы решать такую

$$\mathbf{\dot{r}} = c\frac{\mathbf{r}}{|\mathbf{r}|} \times \mathbf{f}\Big(c\frac{\mathbf{r}}{|\mathbf{r}|}\Big),\quad c=|\mathbf{r}_0|$$

[/quote]

[Someone]

Legioner93 в сообщении #1256429 писал(а):

Или лучше даже так: на каждом шаге будем выбирать полярную с.к., у которой

Боюсь, это усложнение приведёт только к куче лишних расчётов. Я ведь не случайно сказал "две-три". Это сведёт преобразования систем координат к минимуму.

Можно попробовать использовать две системы координат, у каждой из которых есть только один полюс. Например, если $R>0$ — радиус сферы с центром в начале координат, то можем определить координаты на сфере $(u_-,v_-)$ и $(u_+,v_+)$ формулами

$$\begin{cases}u_-=\frac x{R-z},\\ v_-=\frac y{R-z},\end{cases}\qquad\qquad\begin{cases}u_+=\frac x{R+z},\\ v_+=\frac y{R+z}.\end{cases}$$

Декартовы координаты $(x,y,z)$ отсюда выражаются с учётом соотношения $x^2+y^2+z^2=R^2$:

$$\begin{cases}x=\frac{2Ru_-}{1+u_-^2+v_-^2},\\ y=\frac{2Rv_-}{1+u_-^2+v_-^2},\\ z=-\frac{R(1-u_-^2-v_-^2)}{1+u_-^2+v_-^2},\end{cases}\qquad\qquad\begin{cases}x=\frac{2Ru_+}{1+u_+^2+v_+^2},\\ y=\frac{2Rv_+}{1+u_+^2+v_+^2},\\ z=\frac{R(1-u_+^2-v_+^2)}{1+u_+^2+v_+^2}.\end{cases}$$

Но выбирать лучший вариант — Вам.