Пусть

— количество способов разбить

баранов на

групп,

. Ясно, что

.
Пусть мы располагаем

бараном. Введём дополнительного барана с минимальной скоростью, что не умаляет общности, в конец цепочки. Этот баран не сможет никого догнать, стало быть, образует отдельную группу, состоящую из самого себя. Остальные

баранов должны тогда образовать

групп, что они могут сделать

способами.
Пусть теперь самый медленный баран введён в цепочку на второе место с конца. В таком случае он отсекает от цепочки группу, состоящую из самого себя и того барана, который будет идти за ним. Но скорость отсечённого таким образом барана можно выбрать

способами, а оставшиеся

баранов должны образовать

группу. Суммарное количество способов для такого положения дополнительного барана

.
Пусть теперь самый медленный баран введён в цепочку на

-тое место с конца. Тогда цепочка рассекается на одну группу, которая будет плестись сзади, численностью

баранов и группировку из

баранов, которая должна образовать

группу. Но скорости отсечённой отстающей группе можно выбрать

способами. Всего способов получить данную расстановку

.
В процессе такого разбиения баранов на подгруппы мы рано или поздно введём дополнительного барана на то место, где численность "лидирующей группы" баранов будет меньше, чем количество групп, которые она должна образовать. Стало быть, способов, которыми можно так сделать, будет нуль, откуда заключаем, что

при
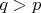
. Заметим дополнительно, что

.
После этих рассуждений можно написать

Искомое в задаче матожидание

количества групп, на которые разобьются

баранов, равно

Получим отсюда рекуррентное соотношение на

:

Введём подстановку

что ведёт к

откуда

Слева стоит сумма

слагаемых, а

, где последнее равенство очевидно. Поэтому естественно положить

, окончательно получая

Используя тот же подход, можно получить рекуррентное соотношение на второй момент

которое той же подстановкой приводится к виду

Дисперсия получается отсюда так:

.



