Пытаюсь понять, как топологически устроена комплексная проективная плоскость

. В частности, хочу получить её симплициальное разбиение.

-- это множество всех одномерных (комплексных) подпространств в
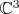
. Первая модель: в
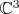
с координатами

рассмотрим единичную сферу

. На

действует группа

следующим образом

. Тогда вся

разбивается на орбиты, гомеоморфные

, и фактор-пространство по этому разбиению и будет

. Допустим, мы имеем достаточно мелкое симплициальное разбиение

, тогда прообраз каждого симплекса

этого разбиения при действии группы будет прямым произведением

. То есть надо разбить сферу

на множества вида

, инвариантные относительно действия группы, и потом из этого разбиения факторизацией получить разбиение

. Плохо представляю, как это сделать.
Еще модель: в
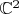
рассмотрим замкнутый шар

, на его граница

действует та же группа

, факторицазия

по которой дает

(расслоение Хопфа). Получается, мы приклеиваем

к

по непрерывному отображению факторизации

. То есть структура CW-комплекса очевидна, но я пытаюсь понять в деталях, как выглядит это приклеивание. Получается в

вложена

, после удаления которой остается

.
Я пытался рассмотреть это в аффинных картах. В карте

с координатами

. Внутренности шара

как раз соответствует аффинная плоскость
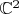
, видимая на этой карте, а границе шара -- бесконечно удаленная прямая

:

, т.е.

. Я рассмотрел эту бесконечно удаленную прямую в другой карте

с координатами

. Бесконечно удаленная прямая

изобразилась в виде прямой

в плоскости
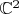
. Это двумерная плоскость

в четырёхмерном пространстве

. В карту не попала одна точка прямой

-- в этой карте она попала на бесконечность. То есть прямая

:

это и есть та самая

, к которой приклеивается граница

. Я попробовал вырезать из


-окрестность прямой

, и склеивать эту

-окрестность с тем, что остается, по границе разреза. Локально, вблизи прямой

, эта окрестность устроена как

, соответственно граница локально устроена как

, но в целом граница, скорее всего будет устроена не как

, а как

. Вот как раз и получается расслоение

на

с базой

. Тоже пытаюсь понять, как же оно устроено. Ломаю голову уже второй день.



