Равномерно распределенная матрица поворота и гауссиана

[artfin]

Добрый день, форумчане!
На днях открыл для себя следующий факт. Я сгенерировал случайную матрицу поворота (в трехмерном пространстве) по алгоритму, представленному в книге D. Kirk. Graphics Gems III (III. 4. Fast random rotation matrices. p.117). Для проверки взял единичные вектора и убедился в том, что они раскидываются равномерно по сфере. Затем проделал следующий эксперимент: взял вектор, координаты которого распределены нормально с $\mu = 0$:

$$ \mathbf{r} \sim \begin{bmatrix} \mathcal{N} \left( 0, \sigma^2 \right) \\ \mathcal{N} \left( 0, \sigma^2 \right) \\ \mathcal{N} \left( 0, \sigma^2 \right) \end{bmatrix} $$

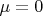
И посмотрел на распределение векторов, которые получаются в результате действия на $\mathbf{r}$ случайной матрицей поворота $\mathds{S}$:

$$ \widetilde{\mathbf{r}} = \mathds{S} \mathbf{r} $$

С некоторым удивлением обнаружил, что компоненты $\widetilde{\mathbf{r}}$ также распределены нормально с такой же дисперсией:

$$ \widetilde{\mathbf{r}} \sim \begin{bmatrix} \mathcal{N} \left( 0, \sigma^2 \right) \\ \mathcal{N} \left( 0, \sigma^2 \right) \\ \mathcal{N} \left( 0, \sigma^2 \right) \end{bmatrix} $$

То есть, действие случайной матрицы поворота $S$ не повлияло на распределение координат вектора. Как это можно доказать?

[Pphantom]

У Вас есть изотропное распределение векторов, которое Вы случайным образом поворачиваете. Естественно, изотропия при этом никуда не девается. Странно было бы, если бы получилось что-то другое.

[artfin]

Да, определенно результат логичный) Но как можно это строго показать? Еще было бы интересно посмотреть на результат, если взять распределение компоненты вектора с ненулевым матожиданием (например): $\mathbf{r}_z \sim \mathcal{N} \left( \mu, \sigma^2 \right)$. На получающееся распределение я глазами посмотрел, но хотелось бы узнать как такие вещи можно выводить, а не "экспериментально" наблюдать

[Pphantom]

artfin в сообщении #1246449 писал(а):

Да, определенно результат логичный) Но как можно это строго показать?

Ну, собственно, из моего первого сообщения ответ на этот вопрос тоже следует. Вам нужно показать, что выбранное распределение векторов является изотропным. Самый простой способ - запись трехмерной функции распределения и тривиальная демонстрация того, что она представима как функция только модуля вектора.

artfin в сообщении #1246449 писал(а):

Еще было бы интересно посмотреть на результат, если взять распределение компоненты вектора с ненулевым матожиданием (например): $\mathbf{r}_z \sim \mathcal{N} \left( \mu, \sigma^2 \right)$.

Вы при этом сдвинете картинку на вектор $\vec \mu$ из начала координат. Соответственно, после поворота качественно ничего не изменится, но компоненты $\vec \mu$ соответстветствующим образом преобразуются.

[Евгений Машеров]

Вы выбрали нормальное распределение. А у него есть приятное и полезное свойство. Линейная комбинация нормально распределённых величин нормально распределена. Умножение на матрицу, любую, есть построение линейных комбинаций. Но тут не любая, а матрица поворота, которая сохранит дисперсию. А так как матожидание у всех было нулевым, то и у комбинации будет нулевым. То есть это свойство прежде всего нормального распределения.
Попробуйте поэкспериментировать с другим распределением. Ну хоть с двусторонним Лапласом, и увидите, что распределение не сохранится, только матожидание и дисперсия, и, скорее всего, будет "нормализация" в смысле приближения распределения к Гауссу.

[ShMaxG]

artfin в сообщении #1246449 писал(а):

Но как можно это строго показать?

1. Формула полной вероятности.
2. Формула преобразования распределения нормального случайного вектора при умножении на матрицу.

[artfin]

Хорошо, сделаю попытку продвинуться.
Обозначим получающуюся случайную величину за $\mathbf{Y}$:

$$ \mathbf{Y} = S \mathbf{X} $$

В силу линейности мат. ожидания:

$$ E \left[ \mathbf{Y} \right] = S E \left[ \mathbf{X} \right] = \mathbf{0} $$

Затем рассмотрим ковариационную матрицу для $\mathbf{Y}$:

$$ Cov (\mathbf{Y} ) = E \left[ \left( \mathbf{Y} - \bar{\mathbf{Y}} \right) \left( \mathbf{Y} - \bar{\mathbf{Y}} \right)^\top \right] = E \left[ \mathbf{Y} \mathbf{Y}^\top \right] = S E \left[ \mathbf{X} \mathbf{X}^\top \right] S^\top = S S^\top = E $$

В случае, когда компоненты вектора $\mathbf{X}$ являются независимыми гауссовыми переменными, ковариация представляет собой единичную матрицу: $Cov( \mathbf{X} ) = E$. А последнее сотношение, гарантирующую единичность ковариации $\mathbf{Y}$, следует из ортогональности матрицы поворота.

[ShMaxG]

artfin
Отлично. Все верно. Но здесь вы предполагали, что матрица $S$ неслучайная. А вот если она случайная, то можно воспользоваться формулой полной вероятности, т.е. проинтегрировать по всем возможным конкретным значениям матрицы $S$. А для конкретных значений матрицы $S$ вы уже поняли, как преобразуется распределение нормального вектора.

[artfin]

Кажется, небольшая описочка вышла. Для моего гауссового вектора матрица ковариации выглядит

$$ Cov \left( \mathbf{X} \right) = \begin{bmatrix} Var ( \mathbf{X}_1 ) & 0 & 0 \\ 0 & Var ( \mathbf{X}_2 ) & 0 \\ 0 & 0 & Var( \mathbf{X}_3 ) & \end{bmatrix} = \sigma^2 E $$

Так что получается важен тот факт, что у всех трех компонент одинаково $\sigma$, потому что иначе не получилась бы ковариация кратная единичной матрице. И именно в этом случае получается, что $Cov( \mathbf{Y} ) = \sigma^2 E$ (если бы ковариация $\mathbf{X}$ не была бы кратна единичной, то она бы не коммутировала с матрицей поворота, и компоненты "замешались" бы).
А в рассматриваемом случае получается, что не имеет значение какое распределение имеет матрица S, т.к. при любом значении матрицы S, результат одинаков. Так?

[ShMaxG]

artfin в сообщении #1247089 писал(а):

А в рассматриваемом случае получается, что не имеет значение какое распределение имеет матрица S, т.к. при любом значении матрицы S, результат одинаков. Так?

Да, и потому что формула полной вероятности.

[Henrylee]

У исходного гауссовсского вектора компоненты брались независимые?