Вы не замечаете, что, ссылаясь на аксиому суммы, Вы выражаете объединение через него же?
Конечно, замечаю. Но такова аксиоматика. Вы предлагаете формулировать задачи на теорию множеств без аксиомы суммы?
Задача состоит в том, чтобы выразить одну операцию через две другие. Использовать в выражении ту операцию, которую нужно выразить, нельзя по смыслу задачи. Разрешены только те операции, которые указаны в условии задачи. И никакие аксиомы тут ни при чём. Они могут использоваться только при обосновании решения.
-- Вт авг 08, 2017 21:24:08 --Если вы не знаете, что такое "математическая индукция", боюсь, доказательства вам даже для подобных задач недоступны.
Не нужна тут никакая математическая индукция.
Спасибо Вам, Someone, что Вы разобрались в самой задаче из учебника!

Вот именно - надо дать определение одного понятия через два других, а не через одно из двух. Я тоже думаю, что это важное замечание.
Да, Куратовский очень интересная личнось. И наверное, он не просто так дал такую задачу в самом начале своей книги - до определения многих других сложных понятий.
-- 08.08.2017, 23:21 --3dmnozhestvotochek, думаю, никто не будет против, если я напишу решение похожей задачи.
Можно ли выразить
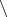
через

и

?
Ответ: нельзя.
Доказательство: докажем, что любое множество, которое можно получить из

и

с помощью

и

содержит все элементы, содержащиеся в

.
Будем доказывать индукцией по числу операций в выражении.
База:

операций - наше выражение либо

либо

, для него утверждение выполнено.
Шаг: пусть нельзя выразить формулой, содержащей меньше чем

операций. Рассмотрим какую-нибудь формулу, содержащую

операций. Последняя (внешняя) операция - либо

, либо

. Если это

, то формула имеет вид

, где

и

получены из

и

с помощью менее чем

операций. Следовательно,

и

содержат

как подмножество, и то же выполнено для

. Аналогично для формулы

.
Рассмотрим теперь

. Тогда

. Следовательно, выразить

с помощью

и

нельзя.
Не нужна тут никакая математическая индукция.
Если расписывать строго, то индукция по длине формулы / числу операций нужна.
Спасибо, спасибо, спасибо! Это очень интересно!
Мне очень приятно пообщаться с человеком, который разбирается в этой области. И по теме. Разбираю Ваш пример.
Куратовскому было бы, наверное, приятно... если он не был зануда.
 -- 08.08.2017, 23:26 --
-- 08.08.2017, 23:26 --В принципе, задача Куратовского практически решена! Если не полностью, то уже практически полностью.
Спасибо!