Задача из учебн. Куратовского, Мостовского "Теория множеств"

[3dmnozhestvotochek]

Доброго времени суток!

Книга К. Куратовского и А. Мостовского "Теория множеств", - М, "Мир", 1970. Только начал читать. Задача 2 в конце 2-го параграфа: 2. Показать, что нельзя определить сумму через произведение и разность, и разность - через сумму и произведение.


Сумма, произведение и разность - имеются ввиду соответствующие операции для множеств (объединение, пересечение и разность).

Странно, что этого сделать нельзя. Два множества могут принадлежать какому-нибудь третьему множеству М, тогда:

A $\cup\ B\equiv(M-[(M-A)\cap(M-B)])$

Или имеется ввиду что никаких других множеств кроме А и В не может больше быть? Даже если 3-го множества нет, то всё равно, используя понятие математического дополнения до 1, можно записать:

A $\cup\ B\equiv(1-[(1-A)\cap(1-B)])$


Выразить разность через сумму и произведение - да, нельзя, видимо. Не получается. Но почему нельзя - не понимаю.

Кто знает, какие критерии можно использовать при решении подобного рода задач?

Спасибо.

[Someone]

3dmnozhestvotochek в сообщении #1239027 писал(а):

Странно, что этого сделать нельзя. Два множества могут принадлежать какому-нибудь третьему множеству М

Вам даны только два множества $A$ и $B$, никакое множество $M$ не задано. Вы можете использовать только те множества, которые можно образовать из $A$ и $B$ с помощью разрешённых операций. Если Вы можете получить требуемое множество $M$, используя только операции пересечения и разности, то используйте его. Если не можете — придётся обойтись без него.

Замечание по поводу терминологии. Слово "принадлежит" употребляется как синоним термина "является элементом", а слово "содержится" — как синоним термина "является подмножеством". Вы уверены, что хотели сказать, что $A\in M$ и $B\in M$? Или Вам всё-таки нужно $A\subseteq M$ и $B\subseteq M$?
Кстати, понятие подмножества появляется только в третьем параграфе, и задачи второго параграфа нужно решать, не используя это понятие.

3dmnozhestvotochek в сообщении #1239027 писал(а):

используя понятие математического дополнения до 1

Что за "математическое дополнение до $1$"? Где Вы в первых двух параграфах нашли множество $1$? Боюсь, Вам придётся обойтись него.

[3dmnozhestvotochek]

Понял. Хорошо.

Извиняюсь, да - я хотел сказать что А и В являются подмножествами (содержатся) в множестве М. Спасибо за замечание.

Значит, согласно условию задачи, заданы только два множества: А и В. Кроме них больше не задано никаких других множеств, поэтому нельзя полагать что А и В могут содержаться в третьем множестве М. А и В могут содержать обще элементы, а могут и не содержать их (но А не содержится в В и наоборот). Разрешёнными операциями над множествами А и В являются только $\cap$ и $\setminus$.

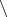
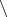
Нужно показать что при помощи операций $\cap$ и $\setminus$ над множествами А и В, нельзя получить выражение для A$\cup$B.

При умножении и вычитании множеств, получаются новые множества которые содержат меньшее количество элементов, чем исходные (либо не содержат никаких элементов, если у А и В нет общих элементов). Поэтому, вычитая и умножая А и В между собой в любой последовательности, нельзя получить сумму А и В, которая всегда содержит больше элементов, чем исходные множества. Как-то так... Логично?

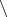
Вторая половина задачи: разность А$\setminus$В нельзя представить в виде $\cup$ и $\cap$. При вычитании получается меньше элементов, чем у исходных множеств А или В. Но у произведения А и В, их ещё меньше... Как быть?

[provincialka]

3dmnozhestvotochek в сообщении #1239118 писал(а):

(но А не содержится в В и наоборот)

Ну почему, может и содержаться. Тут главное, что ваша формула должна давать правильный ответ во всех случаях.

-- 08.08.2017, 13:35 --

3dmnozhestvotochek в сообщении #1239118 писал(а):

При вычитании получается меньше элементов, чем у исходных множеств

Неудачная формулировка. Множества могут быть и бесконечными, так что сравнивать их по "числу элементов" нельзя.

[realeugene]

3dmnozhestvotochek в сообщении #1239027 писал(а):

Странно, что этого сделать нельзя.

Согласен, это, действительно, очень странно, так как существование объединения - это одна из аксиом теории множеств.
Пусть M - это такое множество - объединение, которое существует в соответствии с определением (возможно, не единственное). Если M не единственное, то выберем из класса таких множеств-объединений одно такое множество, пользуясь аксиомой выбора. Тогда $A \cup B\equiv(M-[(M-A)\cap(M-B)])$. Определённая таким образом операция непротиворечива, если её результат не зависит от $M$. Но результат не зависит от $M$.

[mihaild]

Есть несколько вариантов, как решать такие задачи. Лучший идейно и попроще технически, но требующий думать - найти какое-то свойство, которое сохраняется при применении данных операций, которому удовлетворяют исходные множества, но не удовлетворяет то, которое нужно получить.
Попроще в смысле размышлений - просто явно выписать все множества, которые можно получить данными операциями (их не так много).

realeugene в сообщении #1239140 писал(а):

так как существование объединения - это одна из аксиом теории множеств

Ничего странного, это вопрос выразимости через какие-то операции (в булевом виде - через $a \wedge b$ и $a \wedge \neg b$). Аксиоматика теории множеств, если и имеет к этому отношение, то весьма отдаленное.

[realeugene]

mihaild в сообщении #1239145 писал(а):

это вопрос выразимости через какие-то операции (в булевом виде - через $a \wedge b$ и $a \wedge \neg b$).

А это, в принципе, возможно, отделить вопросы выразимости операций над какими-то объектами от аксиоматики самих объектов? Разве, аксиоматика теории множеств тут не подразумевается?

Тут формальная проблема может быть в другом. Откуда следует, что класс множеств-объединений $\Bbb M$ - множество? Очевидно, нужно предварительно доказать, пользуясь аксиомой объёмности, что любые два множества-объединения равны. И тогда аксиома выбора не понадобится, так как $M$ - единственное множество для заданных $A$ и $B$.

[mihaild]

Тут вопрос в том, какие средства нам доступны. Формально можно сказать, что у нас есть функциональные символы $\cap$ и $\setminus$, интерпретируемые понятно как, и хочется выразить через них терм, задающий $\cup$.
Задача, можно ли выразить через них предикат, задающий $X = A \cap B$ - уже другая (очевидно, что в такой постановке нет - нужен хотя бы один предикатный символ).

[realeugene]

mihaild в сообщении #1239152 писал(а):

можно ли выразить через них предикат

Что означает термин "выразить"? Нам не потребуется при этом прибегать к той же аксиоматике теории множеств, например, к аксиоме объёмности, чтобы логически определить равенство функций или предикатов на множествах?

С тем, что вопрос в доступных средствах, я полностью согласен. При её решении студенту допускается пользоваться только теми средствами, которые автор учебника изложил ранее. Если серьёзно, задачу, конечно, стоило бы сформулировать следующим образом: можно ли записать функцию от двух аргументов, равную объединению множеств-аргументов, используя в записи только операции пересечения, разности и две переменные - аргументы этой функции.

[Someone]

realeugene в сообщении #1239140 писал(а):

Согласен, это, действительно, очень странно, так как существование объединения - это одна из аксиом теории множеств.

Причём тут аксиомы? Нас просят выразить операцию объединения двух множеств через операции пересечения и разности множеств. А мы отвечаем: "Объединение существует по аксиоме суммы!" А нам скажут: "Ну и пусть существует. А выразите-ка её через пересечение и разность!"

Вы не замечаете, что, ссылаясь на аксиому суммы, Вы выражаете объединение через него же?

[realeugene]

3dmnozhestvotochek в сообщении #1239027 писал(а):

Кто знает, какие критерии можно использовать при решении подобного рода задач?

Построить контрпример. Возьмите для $A$ и $B$ в качестве возможных значений множество подмножеств множества $\left\{ 1 \right\}$, постройте функции в виде таблиц для всех возможных сочетаний операций и покажите, что среди этих таблиц нет таблицы, соответствующей таблице объединения ваших множеств.

-- 08.08.2017, 16:54 --

Someone в сообщении #1239163 писал(а):

Вы не замечаете, что, ссылаясь на аксиому суммы, Вы выражаете объединение через него же?

Конечно, замечаю. Но такова аксиоматика. Вы предлагаете формулировать задачи на теорию множеств без аксиомы суммы?

(Оффтоп)

Как говорилось в анекдоте про золотую рыбку: "чётче нужно формулировать условия задачи".

[mihaild]

realeugene в сообщении #1239154 писал(а):

Нам не потребуется при этом прибегать к той же аксиоматике теории множеств, например, к аксиоме объёмности, чтобы логически определить равенство функций или предикатов на множествах?

Чтобы написать строчку, нам не нужны аксиомы теории множеств вообще. Они нам понадобятся, чтобы сформулировать, что мы хотим задать этой строчкой, и доказать, что мы задали именно то, что хотели.

[realeugene]

mihaild в сообщении #1239173 писал(а):

Они нам понадобятся, чтобы сформулировать, что мы хотим задать этой строчкой, и доказать, что мы задали именно то, что хотели.

Вот именно. Без ZFC написанная строчка бессмысленна.

3dmnozhestvotochek
Рекомендую написать сюда ваше максимально строгое и формальное доказательство невыразимости. Для проверки.

[3dmnozhestvotochek]

Привет всем!

Вот - кажется, решилось! Если есть ошибка - прошу сообщить.

Задача: 2. Показать, что нельзя определить сумму через произведение и разность, и разность - через сумму и произведение.

Дополнительные условия: Заданы только два множества А и В. Разрешены только опреции $\cap$ и $\setminus$ для определения суммы $\cup$, и операции $\cap$ и $\cup$ для определения разности $\setminus$.

Решение: Сумма А и В содержит все элементы, принадлежащие А и все элементы принадлежащие В. Произведение и разность множеств содержат не все элементы, принадлежащие А и В, а только некоторые. Поэтому, в какой бы последовательности не умножали и не складывали множества А и В между собой, не получится результат, содержащий в себе все элементы, принадлежащие А и все элементы принадлежащие В. Сумму нельзя выразить через произведение и разность.

Разность сод. те элементы, кот. содержатся в одном из 2-х множеств и не сод. в другом. Операции $\cap$ и $\cup$ приводят к появлению новых множеств, кот. содержат элементы принадлежащие только обоим множествам - и А и В. Поэтому, каким бы образом мы не объединяли и не умножали множества А и В между собой, результат будет сод. элементы, принадлежащие обоим множествам - и А и В. Поэтому, разность нельзя выразить через сумму и произведение.

[realeugene]

3dmnozhestvotochek в сообщении #1239211 писал(а):

Поэтому, в какой бы последовательности не умножали и не складывали множества А и В между собой, не получится результат, содержащий в себе все элементы, принадлежащие А и все элементы принадлежащие В.

Пусть $A=\{1\}$, $B=\emptyset$. Тогда $A \cup B=A \setminus B$, что противоречит вашему утверждению.

Кроме того, выражение может быть сколь угодно длинным (но конечным). Вы же рассмотрели только отдельные операции.