Сечение поверхности второго порядка плоскостью

[antonz]

Здравствуйте!
Хочу задать несколько вопросов на примере задачи:
"Найти центр, фокусы и директрисы линии пересечения цилиндра $\frac{x^2}{64}+\frac{y^2}{36}=1$ и плоскости $4y+3z=0$"

Единственное, что мне приходит в голову, это выразить $y$ из уравнения плоскости и подставить в уравнение цилиндра, получить уравнение окружности $\frac{x^2}{64}+\frac{z^2}{64}=1$ и выписать для неё требуемые параметры.

Вопросы:
1. Корректно ли так искать пересечение, какие слова при этом надо говорить? Можно ли по другому?
2. Из чертежа видно, что в сечении эллипс, а у меня получлась окружность. Это проекция того эллипса на $XOZ$? Если да, то почему так вышло?
3. Теперь мне нужно спроецировать эту окружность на секущую плоскость, получить эллипс и для него искать требуемые в задаче вещи? Как проецировать?
4. Спроецировав, я получу требуемые параметры в некоторой двумерной системе координат на секущей плоскости, ответы оставлять в ней?
4. Задача трехмерная, значит и уравнения директрис записывать как уравнения прямых в пространстве?

Уточнить условие мне не у кого, а решать подобные задачи жизненно необходимо.

Надеюсь на Ваше понимание.
Спасибо

[arseniiv]

antonz в сообщении #1238430 писал(а):

получить уравнение окружности $\frac{x^2}{64}+\frac{z^2}{64}=1$

Нет, это тоже цилиндр; притом это другой цилиндр, дающий то же пересечение с данной плоскостью. Окружность у него в сечении с плоскостями $y = \mathrm{const}$. Или, как вы написали, в проекции (надо думать, ортогональной) на плоскость $y = 0$ (но лучше говорить о сечениях — был бы эллипсоид или гиперболоид — ситуация была бы сложнее).

antonz в сообщении #1238430 писал(а):

Если да, то почему так вышло?

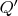
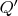
А вот, кстати, интересный вопрос, и вы, в принципе, могли бы на него ответить. Пусть уравнения цилиндра и плоскости выше имеют вид $P(x,y,z) = 0$ и $Q(x,y,z) = 0$ для каких-то многочленов $P, Q$. Вы делаете в этих многочленах линейную замену, оставляющую нули $Q$ на месте; получаются $P'$ и $Q'$, что можно сказать про множества нулей $P'$ и $Q'$ и их пересечение?

antonz в сообщении #1238430 писал(а):

3. Теперь мне нужно спроецировать эту окружность на секущую плоскость, получить эллипс и для него искать требуемые в задаче вещи? Как проецировать?
4. Спроецировав, я получу требуемые параметры в некоторой двумерной системе координат на секущей плоскости, ответы оставлять в ней?
4. Задача трехмерная, значит и уравнения директрис записывать как уравнения прямых в пространстве?

Может, просто задать плоскость параметрически? Так вы получите два вектора, составляющие базис её линейной части и точку, через которую она проходит; можно будет ввести координаты на ней $x', y'$ и работать с ними. После всех манипуляций можно выразить их через исходные, и всё выйдет само собой.

[redicka]

antonz , решив систему, из заданных двух уравнений, вы получите параметрические уравнения эллипса, лежащего в заданной плоскости.
Проекции на плоскости координат будут - эллипс, окружность и прямая.

[arseniiv]

redicka в сообщении #1238438 писал(а):

Проекции на плоскости координат будут - эллипс, окружность и прямая.

Прямая никак не может получиться, только отрезок.

[svv]

Рекомендуется использовать симметрии.

[redicka]

Цитата:

Прямая никак не может получиться, только отрезок

Уравнение отрезка... ?

[antonz]

Большое спасибо за ответы.

Я так понимаю, система координат которую я задаю на секущей плоскости обязательно должна быть ортонормированной, иначе фокусы, директриссы я не найду? Более того, в этой системе уравнение эллипса должно иметь канонический вид (иначе придется к нему приводить)? В данном примере, в силу того, что цилиндр уже приведен к главным осям, а секущая плоскость параллельна оси $x$ нужные базисные направления угадываются легко. В общем случае необходимо было бы приводить пересечение к главным осям?
Можно ли говорить, что когда я строю базис в секущей плоскости, я нахожу вырожденную линейную замену, которая проецирует на секущую плоскость? Если так, то как мне вернуться к начальным координатам, чтобы записать ответ, ведь у вырожденной замены нет обратной?

redicka в сообщении #1238438 писал(а):

antonz , решив систему, из заданных двух уравнений, вы получите параметрические уравнения эллипса, лежащего в заданной плоскости.
Проекции на плоскости координат будут - эллипс, окружность и прямая.

Решив как? Спроецировав на секущую плоскость, я получаю обычное (не параметрическое) уравнение эллписа в координатах этой плоскости.

svv в сообщении #1238455 писал(а):

Рекомендуется использовать симметрии.

Уточните пожалуйста, я не понял)

[svv]

Следующие замены в уравнениях не меняют их (или дают эквивалентные уравнения):
1) $(x,y,z)\to(-x,y,z)$
2) $(x,y,z)\to(x,-y,-z)$
Это значит, что обе фигуры переходят в себя при:
1) отражении относительно плоскости $Oyz$;
2) повороте вокруг оси $Ox$ на полоборота.

Отсюда следует, что центр эллипса и его оси тоже не меняются при таких преобразованиях. Фокусы либо переходят в себя, либо каждый фокус переходит в другой фокус. Значит, центр эллипса находится в точке $(0,0,0)$, одна ось эллипса лежит на оси $Ox$, другая на пересечении плоскостей $Oyz$ и $4y+3z=0$. Вершины лежат на пересечении осей и цилиндра. Значит, можно легко записать их координаты и сказать, какая большая, какая малая.

[arseniiv]

(Оффтоп)

redicka в сообщении #1238500 писал(а):

Уравнение отрезка... ?

Что вы понимаете под этим лаконичным «уравнение отрезка…»? (Какая вообще разница, есть ли у отрезка уравнение? Если спроецировать эллипс на какую-то плоскость ортогонально его собственной плоскости, получится отрезок, а не прямая, и это очевидно.)

[Aritaborian]

antonz в сообщении #1238580 писал(а):

система координат которую я задаю на секущей плоскости обязательно должна быть ортонормированной

А зачем делать из неё другую-то, раз уж она изначально такова? Для решения достаточно преобразований, оставляющих систему координат прямоугольной ортонормированной. Или у вас есть какие-то интересные идеи?

[redicka]

Выглядит это так: