grizzlyок, понял.
-- 25.07.2017, 15:14 --Задача 4*.
Всякое открытое множество есть либо прямая, либо объединение не более чем счетного числа попарно непересекающихся интервалов и открытых лучей.
К этому моменту уже должна была быть счётность

, и тогда никакой звёздочки. Если же этой счётности ещё не было, то задача недобросовестна.
Не обратил внимания на слово "непересекающихся". В этом случае звёздочка всё же есть, пусть и маленькая. Тогда просто надо для каждого числа выбирать максимальный интервал, с соотв. притопами и прихлопами (в них и звёздочка).
Счетности

в виде отдельной задачи не было, но она следует из задачи 10 листка 4: объединение счетного числа счетных множеств счетно. Кажется обсуждали это в какой-то из моих тем.
Вот доказательство задачи 4.
Вся числовая прямая

, очевидно, является открытым множеством.
Возьмем теперь открытое множество

, не являющееся прямой

.
Если

не ограничено сверху, и все точки на прямой

справа от некоторого числа

принадлежат

(т.е. начиная с

нет разрывов:

), то берем открытый луч

. Аналогично, если

не ограничено снизу и не содержит разрывов от некоторой точки

до

, берем открытый луч

.
Никакая окрестность точек

не принадлежит

из-за разрывов слева от

и справа от

. Следовательно, сами точки

также не принадлежат открытому множеству

.
Пронумеруем теперь все рациональные точки

(это позволяет сделать счетность

), не принадлежащие ни одному из открытых лучей

,

, в последовательность
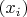
. При этом "склеиваем" те рациональные точки

, между которыми нет разрыва (т.е. все числа между этими точками содержатся в

) -- берем наименьшую из таких точек. Теперь для каждого

возьмем максимальный интервал, содержащий

и целиком принадлежащий множеству

. Получим не более чем счетное число интервалов.
Аналогично началам

открытых лучей, концы взятых интервалов не принадлежат

.
Таким образом,

есть объединение не более чем счетного числа попарно непересекающихся интервалов и открытых лучей.
-- 25.07.2017, 15:45 --Пересечение состоит более, чем из одной точки?
Полагаю, в таком случае пересечение само является интервалом
Доказательство?
Кажется для этого достаточно записать формулу пересечения.
Пусть

-- некоторая система вложенных интервалов, и пусть

,

.
Что такое пересечение:

(тут очевидно, что грани сами не могут входить в пересечение, поэтому неравенство строгое). Видно, что это интервал.
Ни один из интервалов не является подмножеством другого?
Тогда это уже не система вложенных интервалов. Если пересечение пусто, то множество его внутренних точек также пусто. Пустое множество является подмножеством любого множества, в т.ч. пустого, так что такое пересечение открыто. Еще возможен вариант непустого пересечения, в этом случае вопрос: может ли оно не быть интервалом? Мне кажется может (например, если у всех интервалов середина общая, левые концы стремятся друг к другу, и правые концы стремятся друг к другу, то пересечение будет отрезком; доказательство этого может быть похожим на доказательство задачи 17 листка 8. Но тут я не уверен, это просто предварительные мысли). В случае пересечения-отрезка, оно конечно не будет открытым.
Правильные мысли есть. Но если у интервалов общая середина, один из них обязательно содержится в другом (или они совпадают).
Формулировка "левые концы стремятся друг к другу" никуда не годится. Говорите о сходимости - чётко объясните, какую последовательность рассматриваете и её предел.
Кстати, в Вашем ответе есть кое-что полезное для предыдущего вопроса.
Я имел в виду например такое: пусть

-й интервал в системе равен

. Тут конечно не "левые/правые концы стремятся друг к другу", это бредовая фраза. Тут левые концы стремятся к нулю, правые -- к

. Пересечение равно

- интервал, и следовательно открытое множество.
А еще может быть

, тогда пересечение равно одной точке

.
Таким образом уточняю: если ни один из интервалов не является подмножеством другого, то их пересечение может быть открытым множеством, а может и не быть.
-- 25.07.2017, 15:55 --Задача 9.
Объединение конечного числа замкнутых множеств замкнуто.
Доказательство.
Пусть

, где каждое из

-х замкнуто,

.
Возьмем произвольную предельную точку

множества

, и пусть
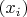
— сходящаяся к

последовательность из точек множества

. Т.к. все члены
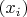
распределены между конечным числом множеств

, то как минимум одно из

-х содержит бесконечное число членов
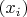
. Пусть это множество

,

. Выделим из
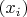
подпоследовательность из членов, принадлежащих множеству

. Эта подпоследовательность также сходится к

(задача 10 листка 11). Следовательно,

является предельной точкой множества

. Таким образом, любая предельная точка множества

является предельной точкой как минимум одного из

-х, и значит по определению

сама содержится в

. Значит,

замкнуто.