Решил трисекцию для любых углов простейшим способом, опроверг теорему Гаусса-Ванцеля о правильных многоугольниках. Вернее, дополнение Ванцеля о невозможности многоугольников, неудовлетворяющих условию, при котором число сторон

, где pi -различные числа Ферма. Надеюсь, верно написал формулу, правила оформления на форуме неудобные. итак. Сначала Гаусс.
Есть метод, который позволяет с помощью циркуля и линейки без делений строить правильные многоугольники с абсолютно ЛЮБЫМ числом сторон. Рассмотрим его на примере правильного девятиугольника.
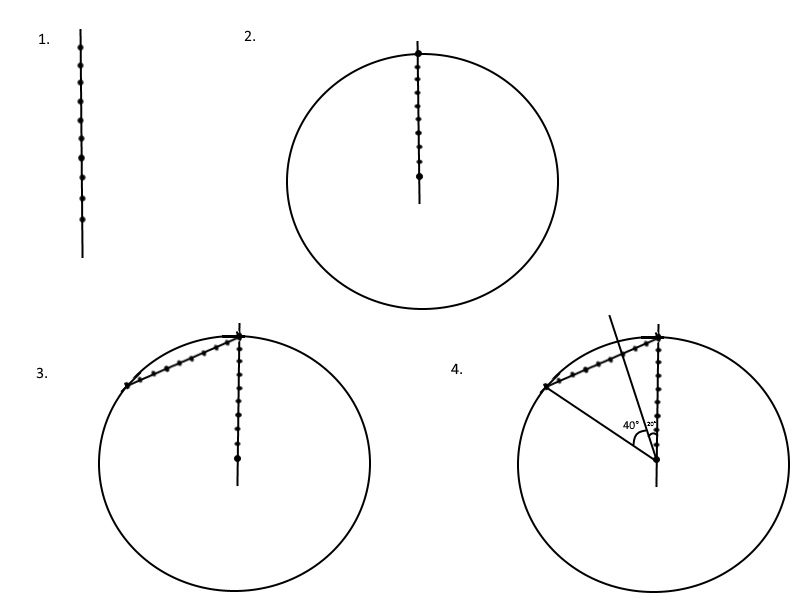
1. Проводим прямую, и с помощью циркуля откладываем на ней девять равных отрезков.
2. Взяв сумму всех отрезков как радиус, строим окружность.
3. Проводим из точки пересечения хорду, равную радиусу, аналогично состоящую из девяти равных отрезков.
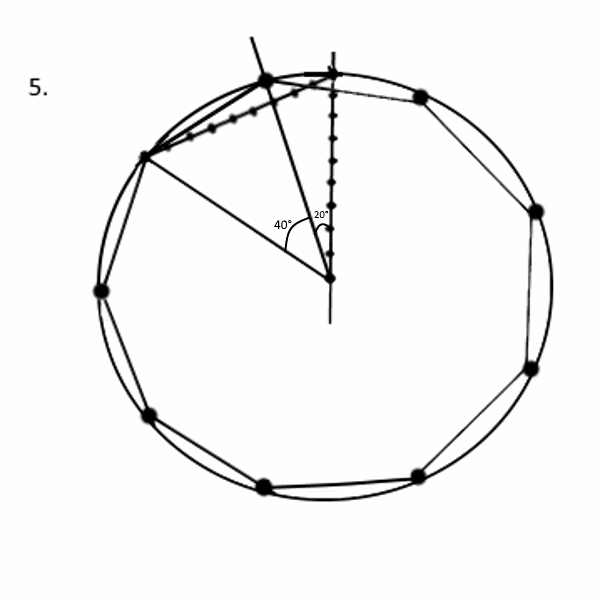
4. Через общую точку шестого и седьмого отрезка на хорде проводим из центра окружности прямую. Также достроим третью сторону равностороннего треугольника из двух радиусов и равной им хорды. Получится, что угол в 60 градусов при центре окружности разделяется прямой на углы в 20 и 40 градусов соответственно.
5. Понятно, что в сущности, задача по построению многоугольника сводится к построению соответствующего угла, который мы уже получили за счет хорды, разделенной на равное количеству сторон искомого многоугольника одинаковых отрезков. Далее, соединив точку пересечения последней проведенной прямой и окружности с дальней вершиной равностороннего треугольника, то есть построив новый треугольник с одним сорокоградусным углом, мы получим сторону искомого многоугольника, откладывая которую внутри окружности, построим этот самый многоугольник.
По этой схеме можно строить без ограничений любые правильные многоугольники, каждый раз проводя таким образом линию из центра через общую точку шестого и седьмого отрезков и аналогично строя хорды. Все дело — в количестве откладываемых мерок. Строятся абсолютно любые многоугольники. метод имеет чуть отличающийся алгоритм для построения правильного пятиугольника: в этом случае нужно получить угол в 72 градуса. Необходимо построить аналогичный радиус и хорду, разделенные на 5 равных отрезков. Это, согласно алгоритму, позволит нам получить пять углов по 12 градусов внутри угла в 60 градусов. Далее один из таких углов нужно добавить к углу в 60 градусов, чтобы получить искомый угол в 72 градуса. Картинка кривовата, но суть будет понятна.
 -- 09.07.2017, 22:39 --
-- 09.07.2017, 22:39 --Теперь интереснее - трисекция.
Задача проста - с помощью циркуля и линейки без делений разделить заданный угол на три равных.
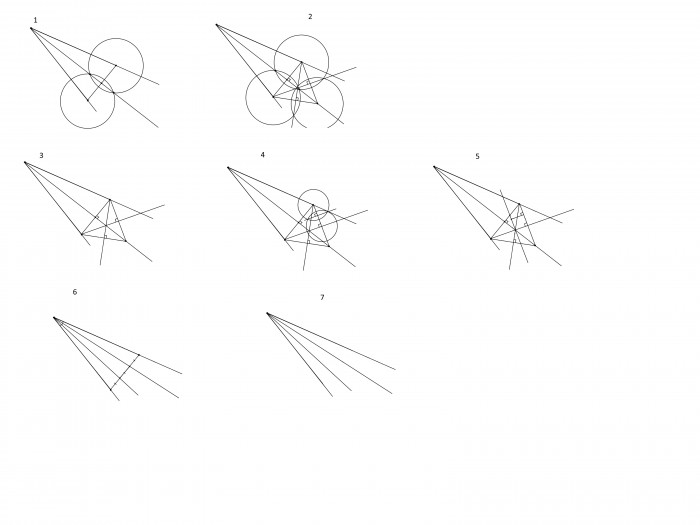
1) С помощью циркуля отметить на лучах угла равные отрезки и соединить их концы. Построить перпендикуляр к получившемуся отрезку, опущенный из вершины угла, используя точки пересечений равных окружностей с центрами в его концах.
2)Отложить от концов отрезка и построить еще два отрезка, равных первоначально построенному так, чтобы одни их концы лежали на опущенном из вершины угла перпендикуляре, а другие - совпадали с концами первоначального. Затем провести в образованном равностороннем треугольнике высоты, используя точки пересечений равных окружностей с центрами в его вершинах.
3)Для удобства убрать вспомогательные окружности, использованные для построения перпендикуляров.
4)Построить еще один перпендикуляр к стороне треугольника.
5) Отложить на нем отрезок, равный меньшей части разделенной центром треугольника высоты. Таким образом, проведенная через его конец и центр треугольника прямая будет параллельна одной из его сторон и точкой пересечения разделит другую сторону в соотношении 1/2, так как в этом же общеизвестном соотношении центр равностороннего треугольника делит высоту.
6)Для удобства и наглядности убрать все лишние построения, оставив только первоначально построенный отрезок с точкой, делящей его 1 к 2. Отложив расстояние этой трети, получить вторую точку. Через полученные точки провести прямые из вершины угла.
7) Убрать все прочие построения, оставив только полученные трисектрисы.
8) В случае, если заданный угол не является острым, его следует произвольно поделить, получив острые углы, проделать с каждым описанную выше операцию и путем сложения долей разделенных на три части первоночально строимых отрезков, отмерить трети первоначально строимого отрезка всего заданного угла, затем аналогично проведя через них лучи из его вершины и разделив его таким образом на три равные части.
 -- 09.07.2017, 22:40 --
-- 09.07.2017, 22:40 --Прошу подсказать, если что то некорректно, так как я не математик. Так, хобби. Посоветовали тут зарегистрироваться и выложить) Так что жду критики)



