1) Подставим

. Если обозначить

, то

.
2) Подставим

. Тогда

. Если

, то подставив

, получим

, и тогда

. Если же

, то
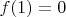
. Дальше будем рассматривать только случай

.
3) Пусть для некоторого

. Подставим

, получим

. Противоречие. Значит

.
4) Подставим

. Получим

. Следовательно, любого

если

, то

.
5) Подставим

, получим

. Следовательно, для целого

верно

. А т.к.
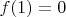
, то для любого целого

верно

.
6) Пусть для некоторого

. Тогда из пункта 4

. Из пункта 3

. Т.е.

.
7) Пусть для некоторых


. Тогда

и для любого целого


. Если

достаточно большое, то

, и тогда

. Подставив эти

, получим

. Из пункта 5 следует, что

. Значит

. Т.е., доказали, что функция инъективна.
8) Возьмем любое

, обозначим

. Из пункта 4

. Применяем теперь утверждение пункта 4 к

, получим

. Но у наc уже

. Из инъективности следует, что

, где

.
Таким образом, Всего существуют три таких функции

, где
