ewertпоражаюсь Вашему терпению со мной.
Мне уже стыдно что я так долго эту задачу мучаю и постоянно ошибаюсь. Вот новый исправленный и дополненный вариант.
Задача 11.
При каких

сходится последовательность

, если
а)

,

Сходимость означает стремление шага

к нулю, которое имеет место быть при

и любом

.
При

и любом

сходимости нет -- из шагов получается арифметическая прогрессия (при

) или неубывающая знакопеременная геометрическая прогрессия (при
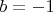
), и первый шаг не равен нулю.
В случае

сходимость возможна только при строгом равенстве шага нулю:

. Найдем всевозможные

, при которых

. Решаем неравенство

. Очевидно,

не подходит. Пусть

. Избавимся от модуля:

. Возведением обеих сторон в квадрат получим

, что верно при любом

. Таким образом, выбрав произвольное отрицательное

и рассчитав

по формуле

, получим сходимость.
Резюмируя, последовательность сходится при независимых друг от друга

и любом

, либо при

и

(в результате будет

).