Если ось

тела

параллельна оси

тела

, значит тело

движется относительно

со скоростью

.
Если ось

тела

(точнее, системы координат, связанной с этим телом), параллельна оси

тела

- тогда, заметьте, все точки на оси

- на мировой линии тела

- будут соответствовать одному и тому же моменту времени на оси

(т.е. относительно

). Это будет означать, что тело

движется не со скоростью

, а с бесконечной скоростью относительно

- потому что за одно мгновение пробегает целую прямую, а в следующие мгновения его уже не существует.
На рисунке

находится в точке

на оси

. Это значит, что для него прошло 6 единиц времени.

же для него находится в точке

. Таким образом

движется относительно

в пространстве

со скоростью

.
Нет! Относительно

, тело

находится в точке

- в какой момент? в момент

(или примерно так - смотрите свой рисунок). Это значит, что тело

прошло (относительно

) расстояние

за время

, то есть его скорость равна

. Так следует читать Ваш рисунок. Но вместе с тем, никакого "бесконечного замедления времени" не наблюдается.
Если же объект B развернется и полетит обратно к A, то в момент встречи в пространстве X, будет находиться ниже по оси T, т.е. окажется, что B будет моложе A.
Я объясню, почему так нельзя думать. Пусть точки

и

имеют одну и ту же координату

, но точка

находится ниже по координате

(пусть у точки

координата

, а у точки

координата

). Вы это трактуете, что тела

и

встретились, причём

моложе

. На самом деле данная ситуация трактуется совсем по-другому: относительно тела

, находящегося в данный момент

в точке

, тело

находилось в той же самой точке

какое-то время назад, в момент

. Где оно сейчас - кто его знает. Ни о какой встрече тут речь не идёт.
Встреча двух тел - это когда их мировые линии пересеклись, а не когда одна точка выше или ниже другой.
А кто из них моложе, кто старее - определяется длиной отрезка мировой линии между двумя встречами. Потому что длина мировой линии - это и есть собственное время. И здесь проявляется псевдоевклидовость: в евклидовом пространстве самый короткий путь - прямой, а в псевдоевклидовом наоборот, прямой путь самый длинный. Поэтому тела, двигавшиеся по прямой, будут старее, а те у которых мировая линия кривая, которые вначале удалялись, потом возвращались - будут моложе.
Я читал о пространстве Минковского, но так и не смог его полностью понять, не смог "представить себя" в таком пространстве.
Вот простое объяснение, что такое псевдоевклидов поворот.
В евклидовом пространстве все направления равноправны, при повороте все поворачиваются одинаково. В пространстве Минковского есть выделенные направления - направления движения со скоростью света. На двумерных картинках

это будут два диагональных направления, под углом 45 градусов к осям координат (если считать

). В настоящем четырёхмерном пространстве-времени эти направления будут образовывать световой конус.
Так вот, при псевдоевклидовом повороте эти направления не поворачиваются вообще. Это соответствует положению, что скорость света инвариантна - то есть объект, движущийся со скоростью

, движется с этой же скоростью в любой системе отсчёта (а переход к другой системе отсчёта - это именно псевдоевклидов поворот).
То есть псевдоевклидов поворот - это поворот с искажением: ось

поворачивается на какой-то угол и превращается в

(или

в

), диагональные направления не поворачиваются вообще, ну а все другие - поворачиваются кто как, кто чуть-чуть, кто побольше.
При этом, понятие перпендикулярности в псевдоевклидовом пространстве тоже своё. Поэтому, когда мы рисуем псевдоевклидово пространство на своём евклидовом листе бумаги, возникает такая вещь: мы можем нарисовать перпендикулярными оси

и

, но тогда оси другой системы,
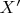
и

- на нашем рисунке уже не будут перпендикулярны. А если нарисуем перпендикулярными
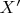
и

- то на таком рисунке не будут перпендикулярны

и

. Эти две картинки, однако, не совсем разные, они переводятся друг в друга псевдоевклидовым поворотом, поворотом плюс искажением.
Скорее всего, это всё, что можно сказать в форумном формате, на пальцах и без иллюстраций.
А кстати, что именно Вы читали о пространстве Минковского? Может быть, здесь Вам посоветуют книги получше.
Не сдавайтесь; пространство Минковского - это не очень сложная штука. Если Вы попытались придумать свой вариант, то попытайтесь сейчас разобраться в настоящем пространстве Минковского. У Вас получится.