Обычно как

Кстати, как-то придумал по аналогии с чем-то, а потом встретил в реальных текстах обозначение

(пригодно вообще для степени любой операции

). Если одинаково часто встречаются и степени композиции, и всякие квадраты-кубы, или просто несколько разных операций на одном и том же, может быть полезно. Другое дело, что у ТС в голове не пойми что.
Как вводятся новые методы в математике (такие как суммирование
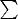
или произведений
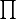
?
Как уже заметили, пока набирался этот пост, это не «методы», а просто обозначения. Все новые обозначения в математике (и других хороших местах) вводятся определением. Другое дело, если вас вдруг интересовали штуки типа

, когда уже известна какая-то конкретная операция с обозначением

— они все определяются одинаково:*
• Если операция ассоциативна, можно взять любое непустое конечное

и определить индуктивно

если

; корректность определения будет гарантироваться ассоциативностью

.
• Если операция имеет нейтральный элемент

, можно доопределить

.
• Для тех семейств

, для которых

конечно, можно определить

и для бесконечных

, беря

вместо

.
•

, где

.
• Ну и если у нас есть пределы, в случае существования и единственности

можно определить

значением предела, однако смысл этой штуки уже заметно отличается от смысла предыдущих, т. к. в них перестановка разных

ничего не изменит, а тут может.
Кажется, других подобных обозначений нет. Заодно пусть меня поправят, если что.
* Не то чтобы я ожидал, что ТС всё это поймёт прям сейчас, базы явно недостаточно.




