Стержень подвешенный за конец (маятник) массы

длины

проходит нижнее положение с угловой скоростью
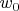
и ударяет нижним концом груз массы

который после удара движется прямолинейно.
Найти угловую скорость

стержня и линейную скорость

груза после удара. Тип удара -НУУ, характеризуемый долей энергии

перешедшей в тепло.
Решение закон сохранения момента количества движения

закон сохранения энергии

где

энерния перешедшая в тепло
сокращая получим систему


подставляя сюда выражение для момента инерции

, обозначая

получим отсюда квадратное уравнение для


при подстановке численных данных оказался положительный дискриминант и 2 положительных корня.
нет объяснения тому ,что получилось 2 значения 
и угловой скорости

.
Где-то ошибка.