Педагогическое коварство аксиомы регулярности я вижу вот в чем. Она запрещает множествам быть элементами самих себя и тем самым сразу избавляет нас от известных парадоксов "множества всех множеств", "множества всех множеств, не содержащих самих себя" и т.д. Кстати, это единственная аксиома, явно придуманная, чтобы что-то запретить - все остальные разрешают.
Ничего подобного. Наоборот, каждая аксиома что-то запрещает, потому что ограничивает свободу в устройстве мира множеств. Мы могли бы рассмотреть мир множеств, в котором нет индуктивного множества — а фигушки, аксиома бесконечности такие миры запрещает. И так далее.
Конкретно аксиома регулярности была последней аксиомой, появившейся в теории ZFC, и появилась она там не для запрещения конструкций, подобных "множеству всех множеств", поскольку связанные с этими конструкциями парадоксы к тому времени были разрешены. Эта аксиома на самом деле утверждает, что класс всех множеств совпадает с так называемым универсумом фон Неймана.
Что касается педагогики, то я считаю, что начинать изучение теории множеств с аксиом категорически нельзя: чтобы понять эти аксиомы, нужно иметь уже весьма большой опыт в теории множеств. По себе знаю.
и объяснял, что никаких "больше из простых арифметических соображений" для символа

в случае бесконечных множеств нет и быть не может, иначе и теоремы Кантора было бы не нужно. Последняя к "простым арифметическим соображениям" отношения не имеет.
Безусловно, арифметика бесконечных кардиналов отличается от арифметики конечных, поэтому и нужны особые доказательства, с этим никто не спорит.
В арифметике бесконечных кардинальных чисел, разумеется, это можно считать "степенью", но это не обычная степень из элементарной арифметики, а символ количества отображений из одного множества в другое (для булеана, очевидно, в множество из двух элементов).
Тем не менее, и для бесконечных кардиналов речь идёт о настоящих произведениях и настоящих степенях — точно так же, как для конечных. Это не просто слова.
В теории множеств есть такая конструкция — произведение индексированного семейства множеств. Она одинаковая и в конечном, и бесконечном случае. Произведение кардиналов — это мощность произведения множеств соответствующей мощности. Если множества одинаковые, получается степень.
Выглядит это так. Пусть

— множество индексов, и каждому
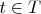
поставлено в соответствие множество

. Тогда произведение

определяется как множество таких отображений

, что

для всякого
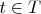
. Это определение одинаково работает и для конечного

, и для бесконечного. И

В случае конечных

и

это теорема комбинаторики, а в общем случае — определение.
Если же

для всех
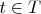
, то пишут проще:

Вот и появляются произведения и степени. В бесконечном случае такие же настоящие, как в конечном.
А множество подмножеств множества

легко отождествляется с

, где

— множество из двух элементов.
Последнее ваше предложение комментировать не собираюсь. Если вы не вчитываетесь в то, что я пишу и на что отвечаю, и хотите к чему-то придираться - ради бога, повод придраться можно найти в любом комментарии.
Извините, если что не так сказал, у меня тоже бывают неточности в формулировках. Но я стараюсь, чтобы их не было.
Ну если уж совсем честно, то

и

-- это разные множества (если определять

и

для

.
Я, собственно, говорю о том, что число элементов произведения множеств

равно произведению чисел

. Разумеется, множества разные, поскольку произведения определяются совсем по-разному.