Доброго времени суток, уважаемые форумчане! Появилась такая вот интересная задача.
Есть изображения пузырей. Задача состоит в том, чтобы определить лежит ли точка (на рисунке - это красные квадраты) во внутренней области эллипса, который можно вписать в образ пузыря, - или не лежит. Примеры когда точки вне пузырей:

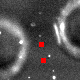
И внутри:

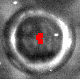

Текущий вариант решения: выделим квадрат заданного размера (скажем, 80x80 пикселей) с центром в рассматриваемой точке.
Бинаризуем изображение внутри квадрата, тогда - получаем двоичный квадратный массив фиксированного размера, как на изображении ниже.

- Я попытался первым делом использовать алгоритм поиска связанных областей (если область нашлась, закрашиваем её и просто проверяем - есть ли внутри неё центральная точка). Однако этот алгоритм весьма и весьма не просто расширить до возможности использования с неполными периметрами эллипсов (точнее я не придумал пока как).. В общем, - такой подход работает, но далеко не всегда (пузыри редко имеют полностью прочерченный обод).
- Также попробовал преобразование Хафа, чтобы подогнать эллипс и определить его размер. Работает - значительно медленнее, но чуть более успешно (для него также непрочерченный обод большая проблема)
Может у кого есть идеи как это сделать лучше и/или быстрее?
Заранее большое спасибо за Ваши комментарии и советы!



