Вроде бы вначале так и говорил - все прямые.
Нет, Вы так не говорили. Перечитайте своё первое сообщение.
Кроме того, то, что Вы написали сейчас — это совсем не то, что написал я. Поэтому ваше "так и говорил"
уже попало в юмористический раздел.
Разве факторизация прямой не приведёт к факторизации плоскости.
Если прямая одна, или речь идёт о множестве попарно не пересекающихся прямых, то особых проблем нет. Но когда прямые пересекаются, строить на них разбиения независимо нельзя, они должны объединяться в одно разбиение плоскости.
Что касается алгебраической структуры на прямой, то думаю, что на всякой прямой евклидовой плоскости не так уж и трудно найти группу по сложению.
Да. И можно найти даже чудовищно большое количество групп по сложению. Какую из них имеете в виду Вы, без телепатических способностей определить невозможно.
Кроме того, создаёт проблемы точка пересечения. Например, как должны быть согласованы разбиения на двух лучах прямой, на которые эта прямая разбита точкой пересечения?
А поточнее описать не можете? Что такое нулевой радиус?
Окружность нулевого радиуса — это просто одна точка, совпадающая с центром. Ну, положите
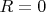
в уравнении окружности

.
Вспомните, что обычно тор (поверхность "бублика") образуют вращением окружности вокруг прямой, лежащей в той же плоскости и не пересекающей окружность. Возьмите предельный случай, когда прямая касается окружности.
Но ещё раз повторю: я совершенно не уверен, что Вы имели в виду именно это. Ваши пожелания настолько невнятны, что понять достоверно ничего нельзя.