Преобразование выражения (A и B) => C

[G00gle]

Выразим импликацию через дизъюнкцию:
$ (A \Rightarrow B) \Longleftrightarrow (\neg (\neg(A \Rightarrow B))) \Longleftrightarrow (\neg (A \wedge \neg B)) \Longleftrightarrow (\neg A \vee B) $

Теперь рассмотрим преобразования более сложного логического выражения:
$ ((A \wedge B) \Rightarrow C) \Longleftrightarrow (\neg (\neg ((A \wedge B) \Rightarrow C))) \Longleftrightarrow (\neg ((A \wedge B ) \wedge \neg C)) \Longleftrightarrow $ $ (\neg ( A \wedge B) \vee C) \Longleftrightarrow ((\neg A \vee \neg B) \vee C) \Longleftrightarrow ((\neg A \vee \neg B) \vee (C \vee C)) \Longleftrightarrow $
$ \Longleftrightarrow ((\neg A \vee \ C) \vee (\neg B \vee C)) \Longleftrightarrow ((A \Rightarrow C) \vee (B \Rightarrow C)) $

В итоге получаем: $ ((A \wedge B) \Rightarrow C) \Longleftrightarrow ((A \Rightarrow C) \vee (B \Rightarrow C)) $
Таблицы истинности для этих равносильных выражений совпадают для всех возможных комбинаций истинности и ложности утверждений $ A, B, C $. Но если попытаться осмыслить это утверждение, то возникают проблемы. Действительно, если достаточным условием для истинности утверждения $ C $ является одновременное выполнение условий $ A $ и $ B $, то это вовсе, как мне интуитивно кажется, не равносильно тому, что $ A $ или $ B $ является достаточным условием для $ C $. Еще понятней это становится, если нарисовать круги Эйлера. Ведь полученное утверждение можно выразить на языке теории множеств: $ (((A \wedge B) \Rightarrow C) \Leftrightarrow ((A \Rightarrow C) \vee (B \Rightarrow C))) \Longleftrightarrow $ $ \Longleftrightarrow (((A \cap B) \subset C) \Leftrightarrow ((A \subset C) \vee (B \subset C))) $
То есть, если пересечение $ A $ и $ B $ лежит в $ C $, то $ A $ либо $ B $ лежит в $ C $. Можно нарисовать эту ситуацию, но там явно получается, что ни одно из множеств $ A $ или $ B $ не должны быть подмножеством $ C $.
К тому же, для похожего утверждения $((A \vee B) \Rightarrow C) $ таких проблем не возникает.
Действительно: $((A \vee B) \Rightarrow C) \Longleftrightarrow (\neg (\neg ((A \vee B) \Rightarrow C))) \Longleftrightarrow (\neg ((A \vee B ) \wedge \neg C)) \Longleftrightarrow $ $ \Longleftrightarrow (\neg ( A \vee B) \vee C) \Longleftrightarrow ((\neg A \wedge \neg B) \vee C) \Longleftrightarrow ((\neg A \vee C) \wedge (\neg B \vee C)) $ $ \Longleftrightarrow ((A \Rightarrow C) \wedge (B \Rightarrow C)) $.
Что вполне логично, так как на языке теории множеств имеем: $ (((A \cup B) \subset C) \Leftrightarrow ((A \subset C) \wedge (B \subset C))) $
Проясните ситуацию, пожалуйста.

[iifat]

Ну, не то чтоб прояснить, но некоторые соображения.
Левая часть ложна в единственном случае: $A$ и $B$ истинны, $C$ ложно.
Правая часть ложна, если ложны обе составляющие, а это снова даёт единственный случай: $A$ истинно, $C$ ложно, и $B$ истинно, $C$ ложно.
Совпадает, не?

-- 01.04.2017, 16:27 --

Подозреваю, вы правую часть как-то не так в термины множеств преобразовали. Хотя, как правильно — что-то не соображу.

[arseniiv]

Проблема в неучёте кванторов.

Единственный правильный способ преобразовывать пропозициональные формулы в утверждения о множествах — это заменять каждую переменную $A$ на $x\in[A]$, где $[\cdot]$ — инъективное отображение пропозициональных переменных в предметные, и $x$ везде один и тот же. После этого уже можно пытаться упростить полученное. Здесь получатся формулы

$$\varphi\equiv[\forall x]\;x\in a\wedge x\in b\to x\in c$$

и

$$\varphi'\equiv[\forall x]\;(x\in a\to x\in c)\vee(x\in b\to x\in c).$$

Попытаемся их преобразовать. Первая действительно преобразуется в то, что писали выше:

$$\varphi\sim \forall x(x\in a\cap b\to x\in c)\equiv a\cap b\subset c,$$

а вот со второй возникают проблемы:

$$\varphi'\not\sim \forall x(x\in a\to x\in c)\vee\forall x(x\in b\to x\in c)\equiv a\subset c\vee b\subset c,$$

хотя одна из этих неэквивалентных формул всё же следует из другой, но только одна (угадайте, какая из какой).

[G00gle]

arseniiv в сообщении #1205628 писал(а):

Проблема в неучёте кванторов.

Единственный правильный способ преобразовывать пропозициональные формулы в утверждения о множествах — это заменять каждую переменную $A$ на $x\in[A]$, где $[\cdot]$ — инъективное отображение пропозициональных переменных в предметные, и $x$ везде один и тот же. После этого уже можно пытаться упростить полученное. Здесь получатся формулы

$$\varphi\equiv[\forall x]\;x\in a\wedge x\in b\to x\in c$$

и

$$\varphi'\equiv[\forall x]\;(x\in a\to x\in c)\vee(x\in b\to x\in c).$$

Попытаемся их преобразовать. Первая действительно преобразуется в то, что писали выше:

$$\varphi\sim \forall x(x\in a\cap b\to x\in c)\equiv a\cap b\subset c,$$

а вот со второй возникают проблемы:

$$\varphi'\not\sim \forall x(x\in a\to x\in c)\vee\forall x(x\in b\to x\in c)\equiv a\subset c\vee b\subset c,$$

хотя одна из этих неэквивалентных формул всё же следует из другой, но только одна (угадайте, какая из какой).

Спасибо большое за ответ. К сожалению, не все понял из того, что вы написали, но общий смысл уловил. Подскажите, пожалуйста, где можно почитать на эту тематику, но, желательно, чтобы книжка была не очень сложной. Не люблю так говорить, но очевидно, что: $ (a\subset c\vee b\subset c) \Rightarrow (a\cap b\subset c) $.
Но почему для формулы $ (((A \cup B) \subset C) \Leftrightarrow ((A \subset C) \wedge (B \subset C))) $ всё работает?

-- Сб апр 01, 2017 13:21:49 --

Выходит, что:

$$(\forall x(x\in a\to x\in c)\wedge\forall x(x\in b\to x\in c))\Longleftrightarrow([\forall x]\;(x\in a\to x\in c)\wedge(x\in b\to x\in c))$$

Поясните, как это получается?

[epros]

iifat в сообщении #1205605 писал(а):

Подозреваю, вы правую часть как-то не так в термины множеств преобразовали. Хотя, как правильно — что-то не соображу.

$(A \cap B) \subset C \Leftrightarrow (A \subset C) \cup (B \subset C)$

arseniiv в сообщении #1205628 писал(а):

Проблема в неучёте кванторов.

Это была задачка на пропозициональную логику, так что кванторы тут ни при чём. И в классической пропозициональной логике равносильность этих двух выражений есть тавтология. В чём увидел проблему ТС непонятно.

Единственный комментарий, который напрашивается, это что указанная равносильность свидетельствует о потере в классической логике связи между импликацией и выводимостью: Если $C$ выводимо в теории с аксиомами $A$ и $B$, это не значит, что оно выводимо или в теории с аксиомой $A$, или в теории с аксиомой $B$.

Вроде, в конструктивной логике эта связь не должна быть потеряна, а стало быть указанная равносильность не должна быть тавтологией. Надо бы проверить...

Но Ваш переход к логике первого порядке тоже интересен. Как я понимаю, он подталкивает нас примерно в том же направлении (я про исследование связи между импликацией и выводимостью).

[iifat]

epros в сообщении #1205660 писал(а):

$(A \cap B) \subset C \Leftrightarrow (A \subset C) \cup (B \subset C)$

Ну дык это ж неверно. В отличие от исходного утверждения.

-- 01.04.2017, 21:03 --

epros в сообщении #1205660 писал(а):

кванторы тут ни при чём

Ни при чём. Пока мы не взялись переводить высказывание на язык множеств.

[epros]

iifat в сообщении #1205666 писал(а):

Ну дык это ж неверно.

Ой, там же ещё значки $\subset$ надо поменять на какой-нибудь $\setminus$, И, соответственно, равносильность - на равенство множеств.

-- Сб апр 01, 2017 15:24:59 --

Точнее, на объединение одного множества с дополнением другого. Такая операция как-нибудь называется?

[arseniiv]

G00gle в сообщении #1205655 писал(а):

Подскажите, пожалуйста, где можно почитать на эту тематику, но, желательно, чтобы книжка была не очень сложной.

Любую, где описывается интерпретация формул первого порядка (логики предикатов).

epros в сообщении #1205660 писал(а):

Вроде, в конструктивной логике эта связь не должна быть потеряна, а стало быть указанная равносильность не должна быть тавтологией. Надо бы проверить...

В интуиционистской логике как раз одна из них будет тоже следствием другой (относительно перевода — та же той же, и это наверняка не просто совпадение, но разматывать эту нить, я думаю, тут ни к чему), но не наоборот. Тут я уподоблюсь sigfpe и переведу всё на хаскель. Если у нас есть функция f :: (a, b) -> c, то мы можем получить функцию значение f' :: Either (a -> c) (b -> c), взяв одну из её компонент: f' = Left . fst . f или f' = Right . snd . f. В обратную сторону же мы пойти никак не можем, нам «недостаточно информации», чтобы взять откуда-нибудь другую компоненту.

Хаскель в данном случае заменяет BHK-интерпретацию пропозициональной логики (когда дело доходит до кванторов, они расходятся).

epros в сообщении #1205670 писал(а):

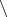
Ой, там же ещё значки $\subset$ надо поменять на какой-нибудь $\setminus$, И, соответственно, равносильность - на равенство множеств.

Вот тогда налёт конструктивности исчезнет, согласен, и всё будет равно.

epros в сообщении #1205670 писал(а):

Точнее, на объединение одного множества с дополнением другого. Такая операция как-нибудь называется?

Боюсь, никак. Хотя я бы не сказал, что она никому не нужна. С ней очевидны такие же проблемы как и с дополнением, когда рассматриваются множества не из какой-то (сигма-)алгебры — будут получаться классы, не являющиеся множествами, и не всегда им рады.

[epros]

arseniiv в сообщении #1205672 писал(а):

В интуиционистской логике как раз одна из них будет тоже следствием другой

Ну, дык, в обратную-то сторону следствия ведь не будет.

Без всякой конструктивной логики: Из $(A \wedge B) \vdash C$ ведь не следует $(A \vdash C) \vee (B \vdash C)$.

[arseniiv]

epros в сообщении #1205677 писал(а):

Ну, дык, в обратную-то сторону следствия ведь не будет.

Да, я хотел написать, что в обратную тоже не будет. Неудобно, что в русском языке нет никакого слова для «в одну сторону следует и в другую не следует» кроме «X сильнее/слабее Y», эта конструкция не везде одинаково хорошо вставляется.

[iifat]

epros в сообщении #1205670 писал(а):

Ой, там же ещё

Ну да, если написать чего-нить другое, то оно, может, и получится по-другому, не поспоришь.