Теорему о том, что наличие модели равносильно непротиворечивости, вы знаете?
Да, конечно, без нее даже смысл задачи было бы трудно уловить.
Попробуйте так. Для начала найдите какую-нибудь теорию

, в которой выводимо как можно меньше всего. Дальше подумайте, что можно взять в качестве

.
Я пока писал пример теории

вроде бы придумал доказательство. Пусть

противоречиво. Тогда

содержит абсолютно все предложения над сигнатурой. Возьмем за

любое предложение из

, тогда

содержит его отрицание. Аналогично для

. Теперь рассмотрим случай, когда ни

, ни

не являются противоречивыми. Если их объединение противоречиво, то значит оно содержит некоторое

и
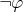
, причем одновременно в

или в

они лежать не могут, в силу их непротиворечивости. Только как доказать, что противоречивая теория содержит все предложения над сигнатурой?



