Однако, дело здесь именно в том, что от конкретного вида этой регуляризации будет зависеть вид вклада в эволюцию от интервала скачка. А это в свою очередь, означает, что при большой "высоте" скачка, (т.е. вне теории возмущений по малой его высоте) когда основной вклад этого временного интервала в эволюцию уже нельзя "выкинуть" из оператора эволюции вместе с высшими порядками разложения Дайсона, - мы не можем уже утверждать , чему именно этот вклад будет равен: выражению

- как писал тут один из участников, или чему-то еще (на самом деле, этот вклад может быть в общем случае вообще равен чему угодно).
А вот и нет.
Cos(x-pi/2) по сути уже всё объяснил, см. пост, цитированный ниже:
Случай с изменяющейся скачком функцией

получается отсюда при

Видно, что в этом пределе вклад в
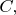
зависящий от

стремится к нулю, т.е. детали поведения функции

в промежутке её изменения перестают влиять на скачок фазы волновой функции в этой задачке.
Можно абсолютно строго показать следующее: возьмём
любую непрерывную функцию

на отрезке
![$[0,1]$ $[0,1]$](https://dxdy-03.korotkov.co.uk/f/a/c/f/acf5ce819219b95070be2dbeb8a671e982.png)
, такую что

,

.
Далее, вместо точки

в исходной задаче вклеим отрезок
![$[t_0,t_0+\varepsilon]$ $[t_0,t_0+\varepsilon]$](https://dxdy-02.korotkov.co.uk/f/9/3/f/93fa5e08aa53bba23762611f9c879e5f82.png)
, и на этом отрезке зададим гамильтониан выражением

. Тогда он будет плавно меняться от

до

с профилем, описываемым функцией

.
Далее, при фиксированном

можно точно решить УШ
в абсолютно классическом смысле, ни единого разрыва, и даже получить точную формулу для решения, в которую будет входить экспонента от интеграла функции

. При конечном

функция будет дифференцируема в классическом смысле при всех

.
Далее, в этой формуле можно устремить

к нулю.
Утверждение: независимо от профиля функции

, решение при

будет сходиться к одному и тому же решению, полученному в первом посте и соответствующему непрерывной регуляризации/решении в обобщённных функциях.
Т. е. от того, как именно происходит скачок, в пределе малости интервала на самом деле вообще ничего не зависит.